Изучение методов оценки генеральных характеристик по выборочным значениям, страница 3

γ

Рисунок 1. - Графики зависимости доверительных интервалов для математического ожидания от числа элементов выборки и заданной доверительной вероятности (1-ая выборка). Для n = 10 – сплошная линия; n = 15 – штриховая линия; n = 20 – точечная линия.

γ

	γ

 

Рисунок 2. - Графики зависимости доверительных интервалов для математического ожидания от числа элементов выборки и заданной доверительной вероятности (2-ая выборка). Для n = 10 – сплошная линия; n = 15 – штриховая линия; n = 20 – точечная линия.

, Ом2

, Ом2

γ

γ

Рисунок 3. - Графики зависимости доверительных интервалов для дисперсии от числа элементов выборки и заданной доверительной вероятности (1-ая выборка). Для n = 10 – сплошная линия; n = 15 – штриховая линия; n = 20 – точечная линия.

Рисунок 4. - Графики зависимости доверительных интервалов для дисперсии от числа элементов выборки и заданной доверительной вероятности (2-ая выборка). Для n = 10 – сплошная линия; n = 15 – штриховая линия; n = 20 – точечная линия.

Условие однородности дисперсий проверяется с помощью критерия Фишера (F):

 .

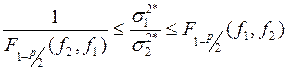Проверка однородности производится для доверительной вероятности γ = 0,95, для выборок из 10, 15 и 20 элементов.

10: ,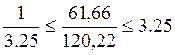

,

15: ,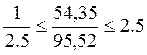

,

20: ,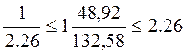

.

Таким образом, поскольку данное условие выполняется, то распределение дисперсий можно считать однородным с вероятностью 0,95.

Условие однородности математических ожиданий проверяется с помощью критерия Стьюдента:

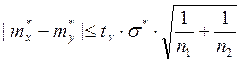, где n₁ – число элементов первой выборки, n₁ = 20;

n₂ – число элементов второй выборки, n₂ = 20;

 - математическое ожидание для первой выборки, = 996,16 ;

 - математическое ожидание для второй выборки =995,50 ;

 - коэффициент Стьюдента, =2,09;

 - средневзвешенная дисперсия;

,

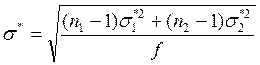, - дисперсии для 1-ой и 2-ой выборок:

Ом²,    Ом².

 - число степеней свободы,

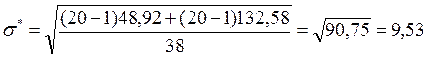Ом,

,

.

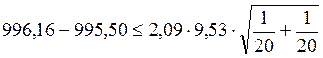Поскольку данное условие выполняется, то можно считать, что математические ожидания однородны.

Анализ полученных результатов:

В ходе лабораторной работы было рассмотрено две выборки резисторов. Найдены математические ожидания, дисперсии и стандарты случайных величин для каждой выборки. Найдены доверительные интервалы для математических ожиданий и дисперсий, определена их однородность.

Анализируя графики можно сделать вывод.

На рисунках 1 и 2 изображены зависимости доверительных интервалов для математического ожидания от числа элементов выборки и заданной доверительной вероятности. Из графиков видно, что при увеличение числа элементов выборки ширина доверительного интервала уменьшается. Значит, повышается точность оценки заданного параметра. При увеличение доверительной вероятности ширина доверительного интервала для математического ожидания увеличивается. Значит, при увеличении доверительной вероятности увеличивается интервал, в котором может находиться искомое значения.

На рисунке 1 данная зависимость видна более четко, чем на рисунке 2. Это может быть связано с тем, что в первую выборку попало большее число значений, которые мало отличаются от номинального значения параметра (сопротивления), т.е. разброс этих значений не такой большой как во второй выборке.

Проверка математических ожиданий на однородность показала, что генеральные математические ожидания можно считать однородными и равными.

На рисунках 3 и 4 видно, что при увеличении числа элементов выборки, ширина доверительного интервала для дисперсии, также как и для математического ожидания, уменьшается. Данная зависимость наиболее четко прослеживается опять для 1-ой выборки (Рисунок 3), что опять говорит о меньшем разбросе значений сопротивлений от номинального значения для первой выборки.

Увеличение же доверительной вероятности приводит к увеличению доверительного интервала для дисперсии, тем самым расширяется область, в которой может находится данный параметр.

Однородность дисперсии проверялась с помощью критерия Фишера. Расчеты подтвердили, что дисперсии для сделанных выборок будут однородны и равны с вероятностью 0,95.

Таким образом, величина доверительного интервала зависит от доверительной вероятности: чем больше доверительная вероятность, тем с большей надежностью можно гарантировать полученный результат и тем в большем интервале значений он может находиться. Увеличение числа опытов при постоянной доверительной вероятности приводит к уменьшению доверительного интервала, т.е. к повышению точности оценки заданного параметра.