Исследование корреляционной связи параметров

Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

«Владимирский государственный университет»

кафедра конструирования и технологии радиоэлектронных средств

Отчет по лабораторной работе №3

«Исследование корреляционной связи параметров»

Выполнил: ст.гр. Р-104

Проверил: профессор кафедры КТРЭС

Владимир, 2006 г.

Цель работы: изучение методики определения корреляционной связи  между параметрами.

1.  Лабораторное задание

1.1.  Провести измерения;

1.2.  Обработать полученные данные в соответствии с методическими указаниями.

2. Краткие теоретические сведения.

Ломаные кривые эмпирической регрессии аппроксимируются прямыми приближенной регрессии:

.

Параметры должны быть такими, чтобы около проведенной прямой наиболее плотно концентрировались все эмпирические точки. Это требование выполняется, если параметры прямой a и b найти по методу наименьших квадратов.

Прямую регрессии, проведенную по методу наименьших квадратов, описывает следующее уравнение:

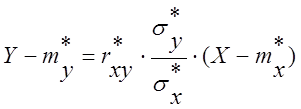, где коэффициент регрессии Y на X .

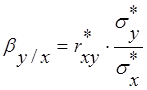Для каждого значения величины Х можно определить соответствующее значение Y по преобразованной формуле:

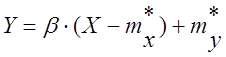
2.  Ход работы

2.1. Исходные данные:

Таблица 1

X	Y	X	Y	X	Y	X	Y
0,89	0,39	16,94	18,5	8,56	9,33	26,32	26,01
1,41	0,74	18,58	19,38	8,78	10,71	26,88	26,49
2,51	1,85	18,7	19,84	9,9	11,3	27,33	26,54
2,55	2,28	19,32	20,3	10,82	11,96	27,75	26,72
3,55	2,39	19,34	20,96	11,87	13,16	28,08	29,43
4,12	2,47	19,8	21,06	13,14	13,18	29,25	29,43
4,38	3,83	20,56	21,54	13,98	13,51	29,83	29,97
4,58	4,13	23,2	21,67	14,94	15,04	24,14	11,78
5,07	4,23	23,91	21,83	14,97	17,43	9,8	27,17
6,75	5,3	24,65	22,49	15,1	17,76	9,35	29,77
7,05	5,96	25,5	23,09	15,35	17,9	10,44	19,12
7,24	6,56	25,84	24,27	15,6	17,97	19,69	27,32
8,32	7,73	26,11	25,27

2.2. По данным таблицы 1 построим поле корреляции и разобьем его на интервалы

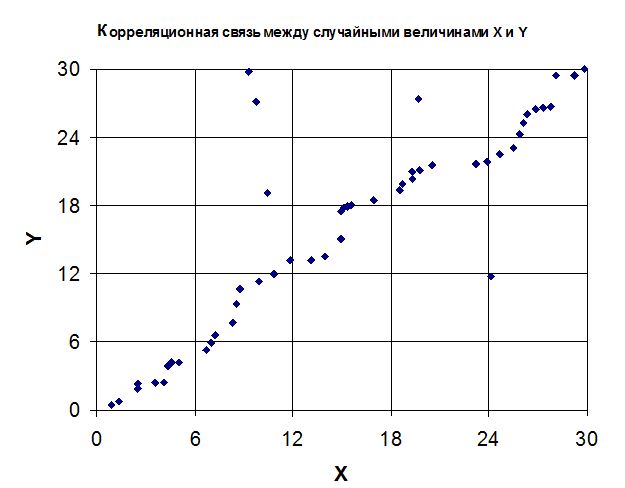
Рис.1 Положительная корреляционная связь между случайными величинами X и Y

Диапазон изменения величин разобьем на интервалы равной длины Dx = 6, Dy = 6

2.3. Найдем количество значений случайных величин, попавших в каждый из интервалов, и занесем их в соответствующие клетки корреляционной таблицы (таблица 2).

Найдем значения x0, y0, которые  выбирают в качестве новых координат отсчета. Затем рассчитаем значения x’ и y’:

 

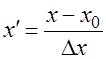
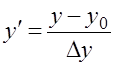
В качестве значений x0, y0 выбираются значения середин интервалов x3,

y3 соответственно.

Значения x, y – середины всех интервалов; Dx, Dy – ширина интервалов.

Таблица2

	x’	-2	-1	0	1	2	ny’	y’ny’	(y’)2ny’	x’y’my’
y’	x y	x1	x2	x3	x4	x5
-2	y1	9+4	2+2	0	0	0	11	-22	44	+40
-1	y2	0	6+1	0	0	1-2	7	-7	7	+4
0	y3	0	1 0	60	0	0	7	0	0	0
1	y4	0	1-1	20	7+1	3+2	13	13	13	+12
2	y5	0	2-2	0	1+2	9+4	12	24	48	+34
nx’		9	12	8	8	13	50	8	112
x’nx’		-11	-12	0	8	26	11
(x’)2nx’		36	12	0	8	52	108
x’y’mx’		+36	+5	0	+9	+40				90

2.4. Найдем коэффициент корреляции, который вычисляется по формуле:

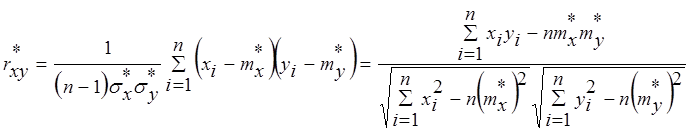
Учитывая, что:

, ;

, ;

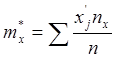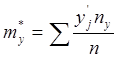Используя данные таблицы 2, получим:

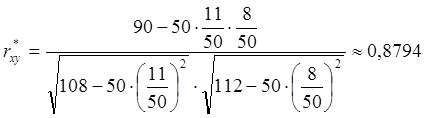
2.5.Определим доверительный интервал коэффициента корреляции. Среднеквадратическое отклонение коэффициента корреляции (при n ³ 30) определяется по формуле:

,

;

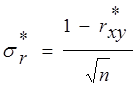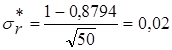Доверительный интервал находят по выражению:

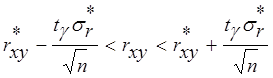, где tg - коэффициент распределения Стьюдента, определяемый по таблицам распределения Стьюдента в зависимости от принятой доверительной вероятности gи числа степеней свободы n-1.

Если g = 0,9,  tg=1,68, то

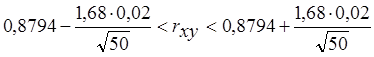
2.6. По полученным данным построим линию регрессии.

Прямую регрессии, проведенную по методу наименьших квадратов, описывает следующее уравнение:

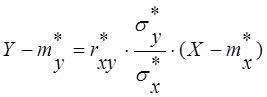, где коэффициент регрессии Y на X:

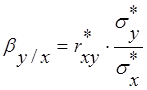
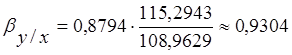
Окончательно получим общий вид уравнения:

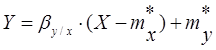
Для нашего случая имеем:

На рисунке 2 показана прямая регрессии

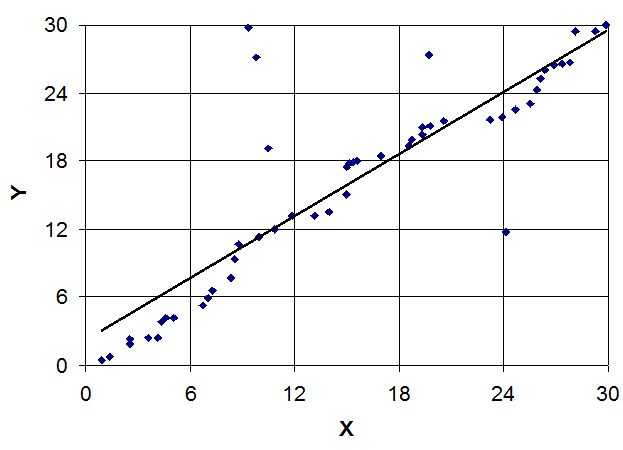
Рис.2 Прямая регрессии

Выводы: В ходе лабораторной работы были изучены методики определения корреляционной связи  между параметрами. Был получен коэффициент корреляции, исходя из которого, можно сказать, чтосвязь величин Y и X близка к линейной функциональной зависимости; был определен доверительный интервал для коэффициента корреляции. Методом наименьших квадратов была построена прямая регрессии, по которой сказать, что связь между случайными величинами X и Y близка к линейной.