Министерство образования Российской Федерации
Владимирский государственный университет
Кафедра конструирования и технологии радиоэлектронных средств
Отчет по лабораторной работе №3
Исследование корреляционной связи параметров.
Выполнил
ст. гр. РЭ-101
Проверил
Владимир, 2003
Цель работы. Изучение методики определения корреляционной связи между параметрами.
Теоретические сведения.
Между случайными величинами могут существовать два вида связи: функциональная и стохастическая (вероятностная). При функциональной зависимости какая-либо величина определяется как однозначная функция одной или нескольких величин. При стохастической зависимости одна из величин реагирует на изменение другой изменением своего закона распределения. Например, стохастической зависимостью связаны между собой затраты на повышение надежности и надежность изделия.
Наиболее важные характеристики случайных величин - математическое ожидание и дисперсия. Систему случайных величин характеризуют совокупности математических ожиданий и дисперсий. Кроме них для характеристики системы случайных величин применяется корреляционный момент, представляющий математическое ожидание произведения центрированных случайных величин.
Особенность корреляционного момента заключается в том, что он характеризует не только рассеивание случайных величин Xи Y, но и связь между ними.
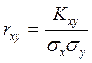(1)
, где 
и 
- средние
квадратические отклонения величин x и y.
Коэффициент корреляции характеризует не всякую зависимость, а только так называемую линейную. Она означает, что при возрастании одной случайной величины другая возрастает (или убывает) по линейному закону. Степень тесноты линейной зависимости определяется величиной коэффициента корреляции, который может принимать значения в пределах ± 1. Если rху= 0, то такие величины называются некоррелированными; если rху = ±1, то величины связаны линейной функциональной зависимостью, возрастающей при +1 и убывающей при -1.
Для оценки линейности связи строят также линии регрессии. Находя для каждого значения одной величины, допустим, X, среднее из соответствующих значений другой величины Y, получаем функцию регрессии, или просто регрессию Yна X. Корреляция между величинами Xи Yназывается линейной, если обе функции регрессии линейны. В этом случае они превращаются в "прямые регрессии".
При построении линий регрессии ломаные кривые эмпирической регрессии аппроксимируются прямыми приближенной регрессии:
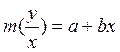(2)
Параметры а и bдолжны быть такими, чтобы около проведенной прямой наиболее плотно концентрировались все эмпирические точки.
Это требование выполняется, если параметры прямой а и Ь найти по методу наименьших квадратов.
При этом методе стремятся, чтобы сумма квадратов отклонений экспериментальных точек от прямой, заданной формулой (2), была минимальной, т.е.
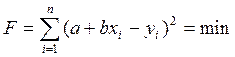(3)
Для выполнения этого условия необходимо, чтобы
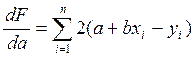
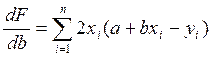(4)
Определение доверительного интервала коэффициента корреляции.
Ввиду ограниченного объема выборки коэффициент корреляции будет определяться с некоторой погрешностью. Для большой выборки (n> 30) среднеквадратическое отклонение коэффициента корреляции.
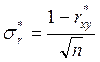(5)
, где n- объем выборки (количество пар измененных значений Х и Y).
Из выражения (5) видно, что относительная
погрешность оценки увеличивается по мере ослабления корреляционной связи и
уменьшения Обычно при rху 
0,3 связь считается практически недостоверной.
Доверительный интервал находят по выражению:
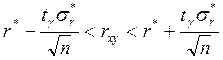(6)
, где ty - коэффициент распределения Стьюдента, определенный по таблицам распределения Стьюдента в зависимости от принятой доверительной вероятности у и числа степеней свободы n - 1.
Обработка экспериментальных данных.
1. Для выполнения лабораторной работы были получены значения параметров X и Y, которые представлены в виде таблицы 1.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
