Изучение методики определения корреляционной связи между параметрами, страница 3

	x`	-4	-3	-2	-1	0	1	2	3	4	5	ny`	y` ny`	y`2 ny`	x`y` my`
y`	x   y	x1	x2	x3	x4	x5	x6	x7	x8	x9	x10
-5,3	y1	1/ 21,2	-	2/ 10,6	-	-	-	-	-	-	-	3	-15,9	84,3	42,4
-4,3	y2	1/ 17,2	-	-	1/4,3	-	-	-	-	-	-	2	-8,6	37	21,5
-3,3	y3	1/ 13,2	1/ 9,9	-	-	-	1/ -3,3	-	-	-	2/ -16,5	5	-16,5	54,5	-13,2
-2,3	y4	-	1/ 6,9	-	3/2,3	1/0	-	-	-	1/ -9,2	-	6	-13,8	31,7	4,6
-1,3	y5	1/ 5,2	-	-	-	1/0	-	-	-	1/ -5,2	1/ -6,5	4	-5,2	6,8	-6,5
-0,3	y6	-	-	-	1/0,3	-	-	-	-	1/ -1,2	-	2	-0,6	0,2	-0,9
0,7	y7	-	3/ -2,1	-	-	-	1/ 0,7	4/ 1,4	-	-	1/ 3,5	9	4,2	4,4	3,5
1,7	y8	-	1/ -5,1	1/ -3,4	-	-	-	-	-	1/ 6,2	1/ 8,5	4	6,8	11,6	6,2
2,7	y9	1/ -10,8	-	2/ -5,4	-	2/0	-	1/ 5,4	-	1/ 10,2	-	7	18,9	51	-6
3,7	y10	1/ -16,8	1/ -11,1	1/ -7,4	-	1/0	1/ 3,7	1/ 7,4	-	-	2/ 18,5	8	29,6	109,5	12,8
nx`		6	7	6	5	5	3	6	0	5	7	50
x` nx`		-28	-21	-12	-5	0	3	12	0	20	35	4
x`2 nx`		96	63	24	5	0	3	24	0	80	175	470
x`y`mx`		29,2	-5,7	-0,4	11,5	0	1,1	18,4	0	0,8	9,5				64,4

3. По данным таблицы 2 рассчитаем коэффициент корреляции и оценим его достоверность.

Эмпирический коэффициент корреляции r_xy находится по формуле:

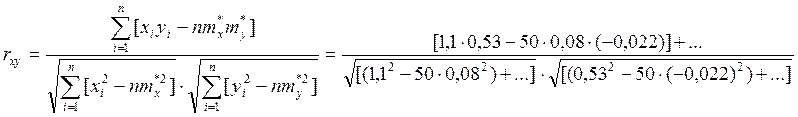 = = 0,124

Доверительный интервал коэффициента корреляции рассчитывается из выражения (6), где 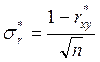 = 0,0269.

Коэффициент распределения Стьюдента  в данном случае ( = 0,9 и n = 50) равен 1,68. Исходя из этого, найдем доверительный интервал:

0,8035<r_xy<0,8163

4. По результатам измерений построим эмпирические линии регрессии:                         

	y

 

x

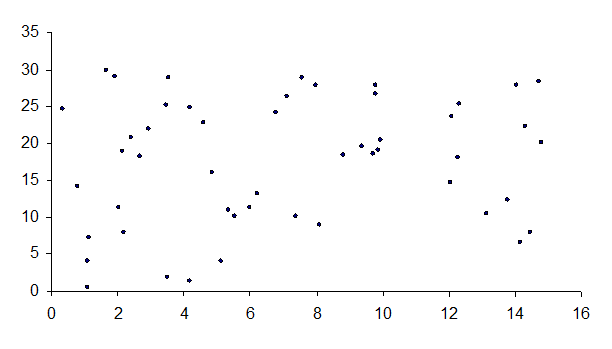
Рисунок 2. Эмпирические линии регрессии.

5. Для нахождения параметров прямых приближенной регрессии применим метод наименьших квадратов. Запишем уравнение прямой регрессии, проведенной по методу наименьших квадратов:

                                                         (7)

, где  - коэффициент регрессии X на Y.

                                                                                    (8)

Преобразуем формулу (7) к виду:

                                                           (9)

Отсюда, параметр а =  = -0,1726, а параметр b =  = 1,8821.

y

По вычисленным параметрам была построена прямая регрессия (рисунок 3).

x

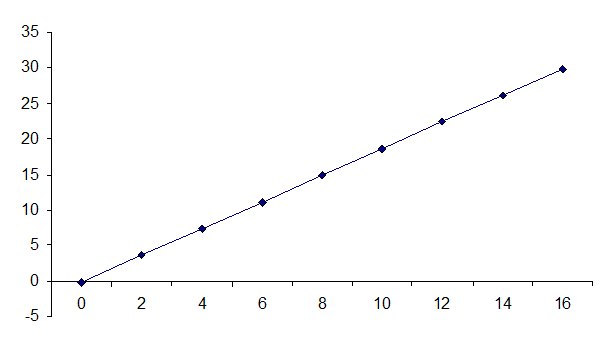
Рисунок 3. Прямая регрессия.