Можно показать, что при работе на N/2-1 периоде (31) более узкое окно Хэмминга позволяет разнести 1-ю и 2-ю гармоники сигнала, но для исключения влияния 3-й гармоники нужно работать на N/2-2 периодах (30). В условиях сильных шумов (10 бит для 12-битного АЦП) даже при работе не на краях диапазона ПЧ более узкое окно Хэмминга по сравнению с окном Кайзера позволяет получить более высокую точность оценки уровня основной гармоники. Погрешности растут при приближении к границам полосы пропускания как снизу, так и сверху за счет затекания спектральных компонент из областей, зеркальных относительно сечений 0 и fд/2. Вблизи нижней границы рабочего диапазона частот во временном интервале оцифровки укладывается малое число периодов сигнала, а вблизи верхней границы рабочего диапазона частот на периоде основной частоты сигнала получается малое число отсчетов – это граница Котельникова.
а) 
б) 
Рис. 5. Особенности расположения спектральных компонент при попадании 1-й гармоники на края диапазона ПЧ
5. Исследование возможностей БПФ для оценки амплитуды основной гармоники по короткой реализации сигнала
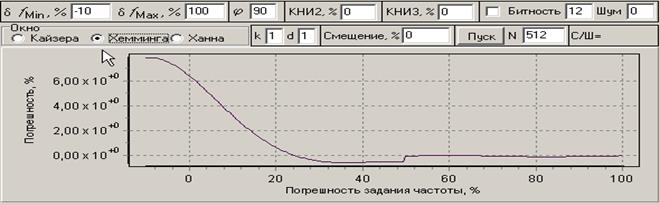
Для более детального исследования влияния отдельных наиболее существенных факторов были созданы две дополнительные моделирующие программы: «Погрешность оценки амплитуды основной гармоники на границах ДПЧ» и «Погрешность оценки амплитуды основной гармоники в зависимости от фазы». На рис. 6 и 7 приведены графики погрешности оценки уровня от погрешности задания частоты сигнала для различных начальных фаз и типов окон при малом числе периодов (k). Графики показывают, что для короткой реализации сигнала в интервале погрешности задания частоты от -10% до 100% наиболее точным является окно Хэмминга, дающее меньшие погрешности оценки уровня. Наименее точным является более широкое окно Кайзера.
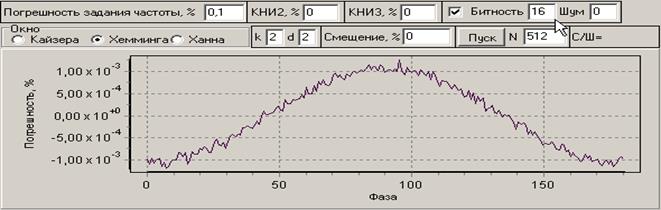
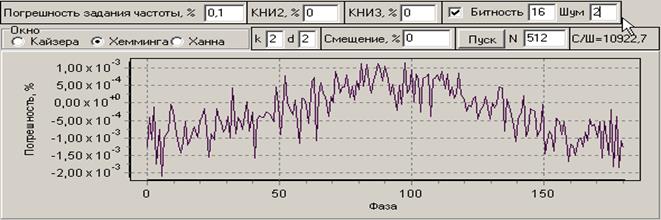
Представленные графики можно рассматривать как графики систематической погрешности, которую, как будет показано ниже, можно скомпенсировать. На рис. 8 и 9 приведены графики погрешности оценки амплитуды основной гармоники от начальной фазы сигнала для различных объемов выборки от 512 до 8192 в условиях ограниченной разрядности АЦП (16 бит) и разного уровня шумов. Из графиков следует, что при коротких реализациях сигнала погрешность оценки уровня сильно зависит от начальной фазы. Но уже при уровне шума 4 бита влияние фазы становится незаметным по сравнения с влиянием шумов. Увеличение объема выборки способствует уменьшению влияния шумов.
а)
б)

в)
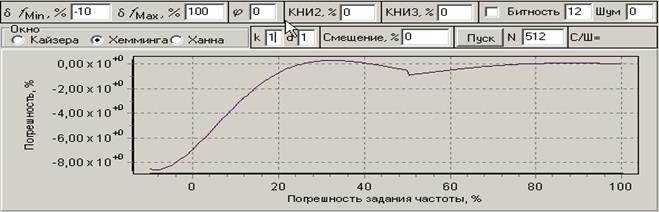
Рис. 6. Погрешности для окна Хэмминга и разных начальных фаз при оцифровке сигнала в интервале времени близком к периоду
а)
б)
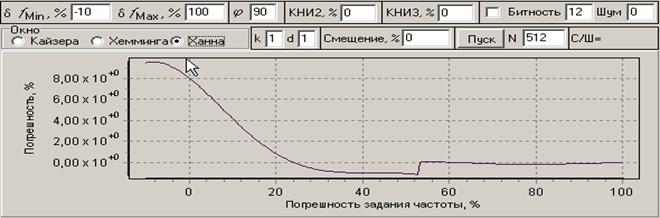
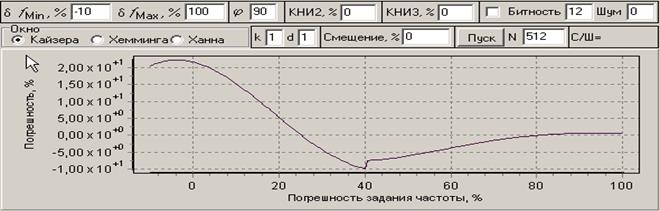
Рис. 7. Погрешности для окон Кайзера и Ханна при оцифровке сигнала в интервале времени близком к периоду
Покажем, что в области коротких реализаций сигнала (1 – 2 периода) и малых шумов можно исключить систематическую погрешность, если предварительно методами анализа массива данных во временной области с достаточно высокой точностью были получены значения рабочей частоты и начальной фазы сигнала. Можно ввести поправочное смещение и оценить уровень с более высокой точностью. Погрешность в этом случае будет зависеть от исходной точности по частоте и фазе с учетом значений крутизны погрешности уровня в рабочих точках, как показано на рис. 10.
а)
б)
в)
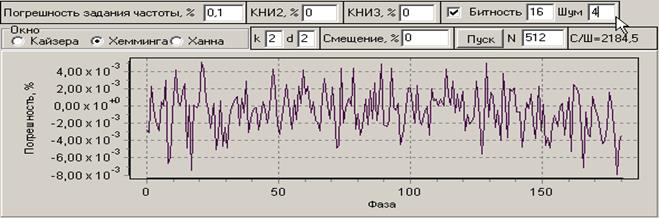
Рис. 8. Погрешности в зависимости от начальной фазы для окна Хэмминга при уровне шума 0, 2 и 4 бит
а)

б)
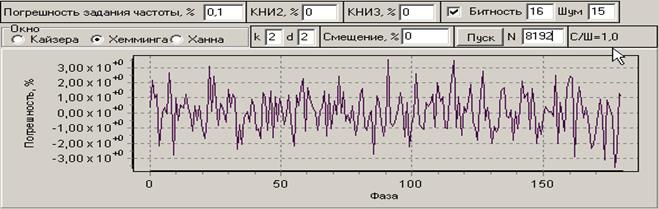
Рис. 9. Погрешности в зависимости от начальной фазы для окна Хэмминга при разном объеме выборки и уровне шумов
а)

б)
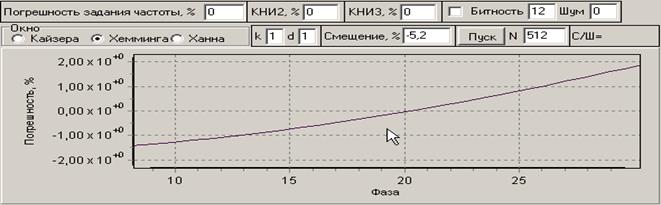
Рис. 10. Оценка влияния крутизны погрешности оценки уровня от исходной погрешности по частоте и фазе
На графиках приведен пример для начальной фазы 00 и одного периода оцифровки сигнала, когда исходные погрешности по фазе и частоте не более 1%. Смещение для заданных условий лучше оценить при отсутствии шумов, оно приблизительно равно –5,2. Влияние исходных погрешностей по частоте и фазе (1%) на погрешность определения уровня можно оценить по графикам соответственно на уровне 0,6 и 0,2% (по модулю). Они независимы, т.е. суммируются под корнем квадратным. Следовательно, полная погрешность не превышает 0,64%. Если для выбранных условий этого достаточно, то методика приемлема для практического применения.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.