3. Анализ амплитудного спектра
Приведем алгоритм оценки СКЗ, исходя из предположения, что первая гармоника сигнала по уровню превышает все остальные. Это позволит реализовать нахождение основной гармоники путем простого сравнения между собой спектральных линий. При необходимости алгоритм можно усложнить добавлением процедуры оценки других наиболее значимых составляющих, выделяемых по уровню или по частоте. Приведем алгоритм [147] оценки СКЗ по шагам:
а) 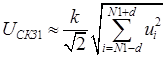 ; б)
; б) 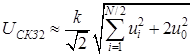 ; в)
; в)
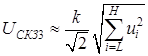 , где ui – амплитуды спектральных компонент; u0 – постоянная составляющая сигнала; N –
число дискретных отсчетов в массиве данных; N1=round(Nf/fд)-
номер спектральной компоненты, соответствующий положению первой гармоники с
разрешением по частоте fд/N; d -
целое число, учитывающее растекание основной гармоники; H=round(NfH/fд)
и L=round(NfL/fд)
- номера спектральных линий,
соответствующих требуемой верхней и нижней границам полосы пропусканияfH и fL;
k – весовой коэффициент, учитывающий влияние
вида используемого временного окна на величину СКЗ сигнала.
, где ui – амплитуды спектральных компонент; u0 – постоянная составляющая сигнала; N –
число дискретных отсчетов в массиве данных; N1=round(Nf/fд)-
номер спектральной компоненты, соответствующий положению первой гармоники с
разрешением по частоте fд/N; d -
целое число, учитывающее растекание основной гармоники; H=round(NfH/fд)
и L=round(NfL/fд)
- номера спектральных линий,
соответствующих требуемой верхней и нижней границам полосы пропусканияfH и fL;
k – весовой коэффициент, учитывающий влияние
вида используемого временного окна на величину СКЗ сигнала.
Для нахождения амплитудного значения гармонического сигнала в приведенной
формуле (а) правая часть умножается на ![]() .
Значение k зависит не только от вида окна, но и
от числа учитываемых спектральных компонент. Например, для окна Кайзера при bk=12 и d=5 оптимальное
значение k=1.971309650, для Ханна k=1.632993162, а для Хемминга k=1.586302719.
.
Значение k зависит не только от вида окна, но и
от числа учитываемых спектральных компонент. Например, для окна Кайзера при bk=12 и d=5 оптимальное
значение k=1.971309650, для Ханна k=1.632993162, а для Хемминга k=1.586302719.
С целью апробации и детального исследования работоспособности приведенного алгоритма была создана компьютерная программа моделирования, которая позволяет оценить степень влияния объема выборки, уровня нелинейных искажений по второй гармонике (КНИ2), вида окна (Кайзера, Хэмминга, Ханна), частоты дискретизации, разрядности АЦП, уровня приведенных к входу АЦП шумов (бит), числа (d), спектральных компонент, учитывающих растекание гармоники сигнала на соседние линии сетки частот ДПФ. Рабочий интерфейс созданной интерактивной программы «Погрешность анализа амплитудного спектра на основе БПФ» приведен на рис. 1. Здесь в окошечке «Битность» не стоит метка, поэтому приведенный график соответствует границам методической погрешности для выбранных условий работы. Если провести огибающие линии сверху и снизу, то внутренняя область будет соответствовать значениям методической погрешности для случайной начальной фазы сигнала.
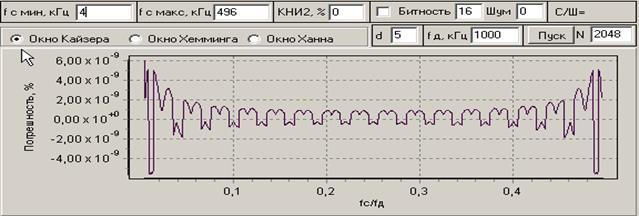
Рис. 1. График максимальной относительной погрешности для N=2048
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.