Моделирование переноса гармоник сигнала в область ПЧ при несихронизированном стробировании, страница 3

Из теории спектров известно, что при изменении масштаба времени электрического сигнала f(t) в q раз масштаб частот спектральных составляющих сигнала меняется в  1/q раз. Таким образом, сжатие спектра  электрического сигнала без изменения его формы возможно лишь при пропорциональном временном расширении этого сигнала. Величину q, показывающую отношение длительности преобразованного  сигнала к длительности входного сигнала, называется коэффициентом трансформации. Такое преобразование спектра и временного масштаба сигнала называется линейным, хотя линейные цепи с постоянными параметрами принципиально непригодны для линейного преобразования временного масштаба электрических сигналов

Для неискаженного линейного преобразования сложного сигнала необходимо, чтобы частоты и амплитуды всех его гармоник в процессе преобразования изменились соответственно в qи K раз, а фазовые сдвиги — пропорционально значениям частоты. Линейное преобразование временного масштаба электрических сигналов произвольной формы возможно в частотно-независимых цепях, осуществляющих задержку сигнала, линейно изменяющуюся во времени по закону . Максимальный сдвиг стробимпульса относительно сигнала при каждом его повторении (шаг считывания Dt) определяется теоремой Котельникова. 

На выходе стробоскопического преобразователя образуется последовательность расширенных импульсов напряжения, огибающая амплитуд которых повторяет форму исходного сигнала. Так как считывание дискретных значений сигнала происходит в течение многих его повторений, то длительность вновь полученного сигнала значительно больше длительности исходного. Выделяя с помощью фильтра огибающую расширенных импульсов, можно получить аналоговый сигнал, идентичный по форме исходному.

Заменить аналоговое стробоскопическое преобразование можно цифровым, реализуемым на уровне вычислительных процедур по данным мгновенных отсчетов сигнала, получаемых с помощью стробирующего АЦП. Пусть на вход АЦП подан периодический сигнал, частота повторения которого незначительно выше или ниже какой-то гармоники частоты дискретизации, а частота высшей гармоники сигнала отличается от ближайшей гармоники частоты дискретизации менее чем на f_д/2. При этом частоты всех составляющих входного сигнала  уменьшаются в одинаковое число раз:

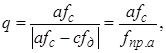
где a и c - заданные целые числа (индексы выборки);  f_пр.а - частота преобразованного сигнала для гармоники а. Приведенное выражение позволяет для q>1 выразить значения частот дискретизации и сигнала:

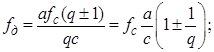
Оценить границы рабочего диапазона частот при восстановлении сигнала во временной области можно по тем же соображениям, что были сделаны в диапазоне 1 (ДИС). Максимальная частота сигнала или его высшей гармоники определяется полосой пропускания АЦП:

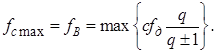
При заданной приведенной к амплитуде погрешности восстановления синусоиды отношение максимального эквивалентного интервала между соседними выборками АЦП  к минимальному периоду сигнала может быть найдено по формуле:

.

При этом предполагается, что точность установки требуемой частоты дискретизации от f_дmin до f_дmax позволяет получить соседние отсчеты со сдвигом . Тогда максимальная частота сигнала или высшей гармоники в спектре сигнала может быть найдена по формуле:

   .

Как и в ДИС минимальная частота сигнала  может быть сколь угодно малой, если реализовать прореживание данных.  Практически можно работать от постоянного напряжения.

Применение вычислительных средств позволяет легко изменить направление оси времени и дополнительно работать в «нижнем» поддиапазоне, когда каждая гармоника сигнала по частоте ниже соответствующей гармоники дискретизации. Только одно это действие расширяет диапазон рабочих частот АЦП в два раза. 

Стробирующий высокочастотный АЦП с регулируемой частотой дискретизации позволяет решить многие проблемы на вычислительном (программном) уровне и реализовать трансформацию спектра и временного масштаба без применения сложных цепей задержки, синхронизации и фильтрации. Современные стробирующие АЦП имеют полосу пропускания до единиц гигагерц при частоте дискретизации порядка сотен мегагерц, что позволяет обеспечить прямой сбор данных в широком диапазоне радиочастот.