Показательная и логарифмическая функции.
1. Значение и место изучения показательной функции
В природе существуют такие процессы, которые не поддаются описанию с помощью алгебраических функций, но с достаточной точностью характеризуются трансцендентными функциями. Среди этих функций важное значение имеют показательная и логарифмическая функции. Показательная функция служит математической формой выражения обширного круга процессов, происходящих в реальной жизни и имеющих общее название процессов естественного роста или убывания величин. Например: численности населения, скорости распада радиоактивных веществ, изменения атмосферного давления с высотой над уровнем моря, падения температуры охлаждаемых тел, скорости размножения бактерий, скорости движения тела в сопротивляющейся среде и т.д.
В раскрытии закономерностей этих процессов используется и логарифмическая функция.
До программы Колмогорова данные функции изучались только в 10 классе, с внедрением в школу программы А.Н.Колмогорова в связи с реформой школы, эти функции были введены в 8 классе и по ныне действующей программе вновь показательная и логарифмическая функции изучаются школьниками в 10 классе сразу после изучения действительных чисел.
Методика изложения данной главы в учебнике последнего издания значительно изменена. Степень с действительным показателем, являющийся необходимым для изучения этой темы, изучается в 1 главе. Введены системы показательных уравнений и неравенств.
2. Определение степени с действительным показателем.
Перед изучением нового представителя из семейства функций учащихся прежде всего необходимо познакомить со степенью с действительным показателем.
Учащиеся знают смысл 25, 20, ![]() и т.д., а что значит возвести число 2 в
иррациональную степень, например
и т.д., а что значит возвести число 2 в
иррациональную степень, например ![]() или
или ![]() , можно ли 0 возвести в степень с действительным
показателем?. Имеет ли смысл выражение
, можно ли 0 возвести в степень с действительным
показателем?. Имеет ли смысл выражение ![]() ?. На
эти вопросы учащиеся смогут найти ответ в ходе беседы, способствующей
повторению определений степени с натуральным, нулевым, отрицательным целым,
рациональным показателем. Беседу эту желательно сопровождать заполнением
таблицы.
?. На
эти вопросы учащиеся смогут найти ответ в ходе беседы, способствующей
повторению определений степени с натуральным, нулевым, отрицательным целым,
рациональным показателем. Беседу эту желательно сопровождать заполнением
таблицы.
|
Определение |
Значение основания |
Обоснование |
Свойства |
|
|
|
При n
четном корень четной степени из отрицательного числа не существует. При |
|
Почему введено
такое определение ![]() при
при ![]() ?
?
С целью сохранения закона умножения степеней:
![]()
аналогично: ![]() ;
; ![]()
Почему введено
такое определение 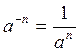 при
при ![]() ?
?
С целью сохранения закона умножения степеней:
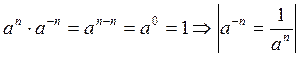
Рассмотрим пример: ![]() .
.
Приближенные
значения ![]() с недостатком
с недостатком ![]() и
приближенные значения
и
приближенные значения ![]() с избытком
с избытком ![]()
По свойству степени
с рациональным показателем ![]() (1)
(1)
![]() (2)
(2)
Рассматривая бесчисленное
множество членов последовательностей (1) и (2) отмечаем, что V
член последовательности (2). Естественно под числом ![]() следует
понимать число, которое больше любого члена последовательности (1) и меньше любого
члена последовательности (2). Без доказательства принимается, что такое число
существует и оно единственное.
следует
понимать число, которое больше любого члена последовательности (1) и меньше любого
члена последовательности (2). Без доказательства принимается, что такое число
существует и оно единственное.
![]() или
или ![]()
Степенью положительного числа с действительным показателем называется предел последовательности степени с рациональными показателями, являющимися приближенными значениями действительного показателя.
Можно рассмотреть существование такого предела на числовой оси.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() при
при ![]() .
. ![]() при
при ![]()
Все свойства степеней с дробным показателем автоматически переносятся на степень с действительным показателем и к пяти известным свойствам:
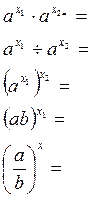 добавляется
шестое свойство:
добавляется
шестое свойство: ![]() при
при ![]() ,
, ![]() , которое затем используется
при доказательстве свойств показательной функции. С помощью свойств степени 1-6
доказываются свойства:
, которое затем используется
при доказательстве свойств показательной функции. С помощью свойств степени 1-6
доказываются свойства:
Т1: при ![]() и
и ![]()
![]()
Т2: при ![]() и
и ![]()
![]()
3. Методические рекомендации к изучению свойств показательной функции.
Прежде всего, необходимо повторить все, что учащиеся
изучали о функции: понятие функции, область определения, множество значений,
возрастающая и убывающая функции, четность, промежутки знакопостоянства, нули
функции. В ходе изучения показательной функции желательно повторить
преобразования графиков функций и уделить внимание построению графиков 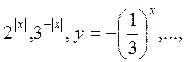 графическому способу решения уравнений и
неравенств, содержащих показательную функцию. Есть возможность для проведения
лабораторно-графических работ. Ч целью повторения преобразований графиков функций
можно использовать графические диктанты с применением шаблонов, кодопозитивов.
При изучении показательных уравнений следует уделить внимание формированию
алгоритмической культуры у учащихся, выполнив соответствующую классификацию
показательных уравнений и составив алгоритм решения уравнений каждого типа.
графическому способу решения уравнений и
неравенств, содержащих показательную функцию. Есть возможность для проведения
лабораторно-графических работ. Ч целью повторения преобразований графиков функций
можно использовать графические диктанты с применением шаблонов, кодопозитивов.
При изучении показательных уравнений следует уделить внимание формированию
алгоритмической культуры у учащихся, выполнив соответствующую классификацию
показательных уравнений и составив алгоритм решения уравнений каждого типа.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.