Показательная и логарифмическая функции. Значение и место изучения показательной функции, страница 2

4.  Некоторые замечания по изучению показательной функции.

Все пять свойств степеней с рациональным показателем учащиеся автоматически переносят на степени с действительным показателем и без доказательства принимается новое свойства (6): при  и , , позволяющее доказать без труда свойство возрастания показательной функции при  и свойство убывания ее при .

1).     (1)

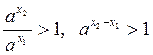 - истина по свойству (6), так как

2).

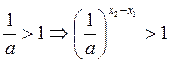 (по свойству 6)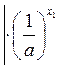   

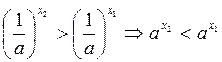
Показательные уравнения и неравенства решаются с использованием свойств степеней и свойств показательной функции, изучение их позволяет еще раз обратить внимание учащихся на алгоритмический характер алгебры.

При изучении показательной и логарифмической функции повторяются и закрепляются преобразования графиков функции, свойств функции, графический способ решения уравнений и неравенств, выполнение лабораторно-графических работ.

Что касается исторических сведений, касающихся данной темы, то здесь можно сообщить следующие факты:

Долгое время понятие степени относили только к неизвестным. В III веке Диофант стал применять сокращенное обозначение неизвестного и степени. Он ввел свои термины для обозначения степеней и особые символы для их обозначения. Диофант называл вторую степень «дюнамис» - сила, третью – «кюбос», четвертую – «дюнамо» - дюнамис,  он обозначал  и т.д.

В XIV веке французский епископ Орем (Орум, 1323-1382) впервые стал применять в отдельных случаях корни из чисел дробными показателями.

Степенью с нулевым показателем первым стал пользоваться самаркандский ученый Ал-Каши в начале XV века. Более подробнее об этом смотри «История математики в школе 9-10 класс» страницы 134-142.

Изобретение логарифмов, название их и первые таблицы логарифмов принадлежат шотландскому любителю математики Джону Неперу (1550-1617), хотя раньше его составил первые таблицы логарифмов также любитель математики часовщик и мастер астрономических приборов швейцарец И.Бюрги (1552-1632), работавший вычислителем с астрономом И.Кеплером. Однако таблицы Бюрги были опубликованы в 1620 г., а таблицы Кеплера появились в 1614 г. Вычислением логарифмических таблиц эти талантливые люди занимались параллельно, но независимо один от другого.

При составлении таблиц они оба руководствовались идеей, высказанной еще Архимедом, а затем более подробно исследованной М.Штифелем в работе «общая Арифметика» (1544 г.). М.Штифель, сопоставив арифметическую и геометрическую прогрессии, указал многие свойства и зависимости двух этих рядов, а затем написал: «Можно было бы, написать целую книгу об этих замечательных свойствах числовых рядов, однако этим ограничусь и пройду мимо с закрытыми глазами» И он действительно прошел мимо возможности применить свойства указанных прогрессий для совершенствования вычислений.

Таблицы Непера значительно упрощали труд вычислителя, но они все же были далеки от совершенства, что признавал и сам автор. Поэтому он вместе со своим другом профессором Генри Бриггсом (1561-1631) занялся составлением десятичных логарифмов. Вычисление этих логарифмов закончил после смерти Непера Бриггс и опубликовал в 1624 году в «Логарифмической арифметике». Четырехзначные десятичные логарифмы Бриггса содержали целые числа от 1 до 20 000.

В 1628 году голландский математик Андриан Влакк дополнил труды непера, он издал десятичные таблицы целых числе от 1 до  100 000. Таблицы логарифмов и логарифмическая линейка, сконструированная на их основе Оутредом (1574-1660 гг.), свыше 350 лет оставались надежным аппаратом для приближенных, но быстрых вычислений.

5.  Несколько рекомендаций к изучению логарифмической функции.

Действующий учебник АиНА – 10-11 написан с учетом того, что с понятием десятичного логарифма учащиеся знакомы с курса А – 8(9). Но в течении последних пяти лет десятичные логарифмы выведены с курса основной школы. Поэтому прежде всего стоит вопрос о пути введения понятия логарифма. Одним из наиболее удачных вариантов введения понятия логарифма является вариант,  изложенный в учебнике А -8 авторы: Макарычев, Миндюк, Монахов и др. (стр. 163)  при  - уравнение не имеет корней.

при  - ед. корень, смотри графическое решение.

Корень уравнения  называется логарифмов числа  по основания . . Логарифм определен только для положительных чисел при положительном основании (разрешимость уравнения ).

Свойства логарифмов рассматриваются традиционно во всех учебниках (  - см. доказательство). Логарифмическая функция вводится абстрактно-дедуктивным путем, ее свойства рассматриваются по стандартной схеме. Тот факт, что  есть обратная функция для  считается не обязательным и большинство учителей этот факт оставляет без внимания. При решении уравнений, неравенств – КСО.

Самостоятельная работа с выборочным ответом.

Лото.

Графические диктанты (преобразование графиков функций).

Тесты:

№1. . Найти число целых решений на (-3;2).

№2.  на промежутке (-1;5)