Другие предметы \ Гидравлика

Определение глубины равномерного движения и ширины канала по дну на подводящем участке канала. Определение средних скоростей движения воды в канале и сравнение их с максимально допустимыми для заданного грунта скоростями

Страницы работы

17 страниц (Word-файл)

Скачать файл

Содержание работы

1. Определение глубины равномерного движения h_o1 и ширины канала по дну b на подводящем участке канала при β = (β _г.н.)_пред.

Основная расчётная зависимость для каналов с равномерным движением воды это формула Шези:

где – средняя скорость движения жидкости, м/с; - коэффициент Шези;

- гидравлический радиус, м; – уклон дна.

Расход жидкости находится по формуле:

где - площадь живого сечения, .

Тогда расход с учетом формулы Шези равен:

В данной задаче в число искомых величин входят - глубина воды в канале и – ширина канала по дну, поэтому эта задача решается путём подбора. Вначале определяется необходимый модуль расхода по формуле:

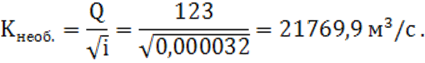
Относительная ширина канала по дну находится по формуле:

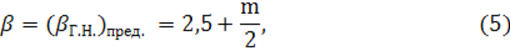
где - коэффициент откоса канала; (β _Г.Н.)_пред – предельное значение относительной ширины канала по дну, при котором площадь поперечного сечения будет минимальной.

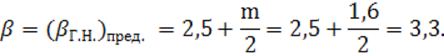
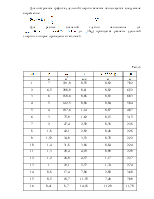
Далее составляется таблица. Задавая глубину потока, будем рассчитывать площадь живого сечения ω, смоченный периметр χ, гидравлический радиус R, коэффициент Шези С и модуль расхода К по следующим формулам:

ω = h²(β+m);

χ = h (β+2Ö1+m²);

R = ω/ χ;

С = 1/n R^1/6;

K = ω C ÖR.

Результаты заносим в таблицу:

Табл 1

Задаваемые и определяемые величины	Ед. изм	Числовые значения
	м	2	4	5	6	7
	м	6,6	13,2	16,5	19,8	23,1
	м²	19,6	78,4	122,5	176,4	240,1
	м	14,1	28,3	35,4	42,4	49,5
	м	1,4	2,8	3,5	4,2	4,8
		48,0	53,9	55,9	57,6	59,1
	м³/с	1107,2	7030,2	12746,7	20727,5	31266,0

Пример расчета столбца№1 ( для

1) ширина канала по дну:

2) площадь живого сечения:

3) смоченный периметр:

4) гидравлический радиус:

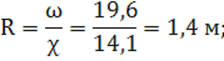
5) коэффициент Шези по формуле Маннинга:

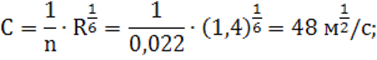
6) модуль расхода:

По таблице 1 строится график зависимости глубины равномерного движения от модуля расхода (рис. 1). Зная находится глубина Ширина канала по дну b= h*β= 6,1*3,3= 20,13 м. Площадь живого сечения

2. Определение глубины равномерного движения на отводящем участке канала , полагая ширину канала по дну

Для отводящего участка канала известно:

· расход воды

· коэффициент откоса

· коэффициент шероховатости

· уклон дна

· ширина канала по дну

Вначале определяется необходимый модуль расхода , для отводящего участка канала, по формуле (4):

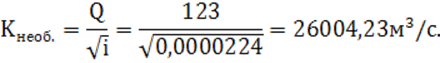
Далее составляется таблица 2, в которой задаются рядом значений h, для которых вычисляются соответствующие модули расхода .

Табл 2

Задаваемые и определяемые величины	Ед. изм	Числовые значения
	м	2	4	5	6	7
	м²	46,66	106,12	140,65	178,38	219,31
	м	27,7	35,2	39,0	42,8	46,5
	м	1,7	3,0	3,6	4,2	4,7
		49,6	54,6	56,3	57,7	58,9
	м³/с	3004,3	10061,8	15035,4	21008,0	28017,2

Пример расчета столбца№1 таблицы 2 ( для

1) площадь живого сечения:

2) смоченный периметр:

3) гидравлический радиус:

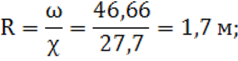
4) коэффициент Шези по формуле Маннинга:

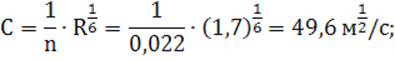
5) модуль расхода:

По таблице 2 строится график зависимости глубины равномерного движения от модуля расхода (рис. 2). Зная находится глубина Далее определяется площадь живого сечения:

3. Определение средних скоростей движения воды в канале и сравнение их с максимально допустимыми для заданного грунта скоростями

Значения средних скоростей на данных участках, при равномерном движении воды в канале, определяются из соотношения (2):

Для подводящего участка:

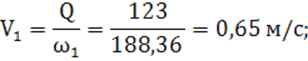
для отводящего участка:

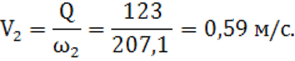
Допускаемая неразмывающая скорость определяется по таблице «Допускаемые неразмывающие донные и средние скорости потока,свободного от коллоидных насосов, для однородных несвязных грунтов(ВТР-П-25-80)» методом интерполирования (таблица 3). Для d = 0,9 мм (d-диаметр частиц песка, слагающего русло канала) допускаемая скорость для потока глубиной более 5 метров будет равна v_неразм= 0,626 м/с. V_{неразм1}=V_{неразм2}=0,626 м/с.

Табл 3

Диаметр частиц , мм	Допускаемые, не размывающие средние скорости в м/с при глубине потока в м
Диаметр частиц , мм	0,5	1	3	5
0,75	0,47	0,51	0,57	0,59
1,0	0,51	0,55	0,62	0,65

V1>(V_max)_доп

V2<(V_max)_доп

4. Определение глубины наполнения и уклон дна канала, полагая

Примем, что b₁=b₂, тогда для подводящего участка канала:

1) определяется площадь живого сечения:

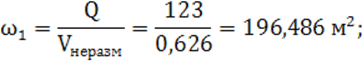
2) определяется глубина наполнения:

3) определяется значение смоченного периметра:

4) определяется гидравлический радиус:

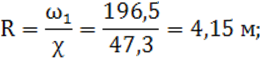
5) определяется коэффициент Шези по формуле Маннинга:

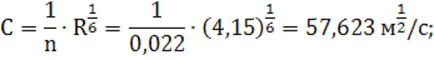
6) определяется уклон из формулы Шези (1):

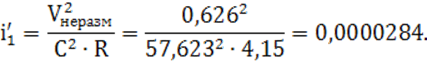
По полученным значениям глубины и ширины, строятся поперечные сечения подводящего и отводящего участка трапецеидального канала (рис. 3).

5. Определение критической глубины и критического уклона

Критическая глубина находится графическим методом, используя следующую зависимость:

где – ширина канала по верху при критической глубине, м; - корректив кинетической энергии; - ускорение свободного падения, м/с².

Далее составляется таблица 4, где для различных глубин находятся значения величин .

Таблица 4.

Задаваемые и определяемые величины	Ед. изм	Числовые значения
	м	0,8	1	1,3	1,5	1,6
	м	23,06	23,7	24,66	25,3	25,62
	м²	17,424	22,1	29,354	34,35	36,896
	м⁶	5289,9	10793,9	25293,1	40530,3	50227,1
	м⁵	229,4	455,4	1025,7	1602,0	1960,5

Пример расчета столбца таблицы 4 для

1) ширина канала по верху:

2) площадь живого сечения:

3) значение величины :

4) значение величины :

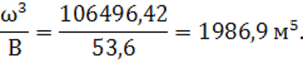
По данным таблицы 4 строится график зависимости (рис. 4). Далее определяется значение величины с учетом зависимости (6), на графике (см. рис. 4) находится критическая глубина

При данной критической глубине определяется:

1) ширина потока по верху:

2) площадь живого сечения:

3) смоченный периметр:

4) гидравлический радиус:

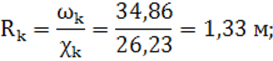
5) коэффициент Шези по формуле Маннинга:

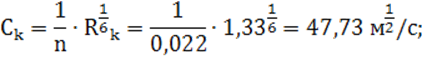
6) критический уклон из формулы Шези (1) и равенства (6):

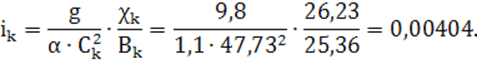
Далее сравнивается критический уклон 04 с уклонами на подводящем и отводящем участках:

· на подводящем участке:

;

· на отводящем участке:

6. Построение графика удельной энергии сечения

Для построения графика удельной энергии сечения используется следующие выражение:

Для разных значений глубин наполнения (от до >h₀₁) проводятся расчеты удельной энергии, которые приведены в таблице 5.

Табл 5


	м	м²	м/с	м	м
1	7	221,9	0,55	0,02	7,02
2	6,5	200,9	0,61	0,02	6,52
3	6	180,6	0,68	0,03	6,03
4	5	142,5	0,86	0,04	5,04
5	4	107,6	1,14	0,07	4,07
6	3	75,9	1,62	0,15	3,15
7	2	47,4	2,59	0,38	2,38
8	1,8	42,1	2,92	0,48	2,28
9	1,52	34,9	3,53	0,70	2,22
10	1,4	31,8	3,86	0,84	2,24
11	1,3	29,4	4,19	0,99	2,29
12	1,2	26,9	4,57	1,17	2,37
13	1	22,1	5,57	1,74	2,74
14	0,8	17,4	7,06	2,80	3,60
15	0,5	10,7	11,55	7,49	7,99
16	0,41	8,7	14,18	11,29	11,70