Определение глубины равномерного движения и ширины канала по дну на подводящем участке канала. Определение средних скоростей движения воды в канале и сравнение их с максимально допустимыми для заданного грунта скоростями, страница 2

Пример расчета таблицы 5 для

1)  площадь живого сечения:

2)  средняя скорость движения воды в канале по формуле (2):

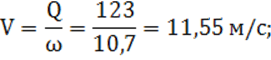
3)  значение скоростного напора  :

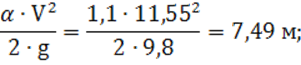
4)  удельная энергия сечения по формуле (7):

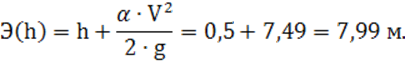
По данным таблицы 5 строится график зависимости удельной энергии сечения  от глубины воды в канале  (рис. 5). Из графика и таблицы видно, что минимальная удельная энергия  (Эmin соответствует h_к).

7. Построение кривой свободной поверхности на подводящем участке канала

Для построения кривой свободной поверхности используют метод Чарномского. В начале задаются различными значениями глубин воды в канале: от  до

Средняя глубина  между поперечными сечениями  и  определяется по формуле:

где ,  - глубины в сечениях  и , м.

Расстояние  межу поперечными сечениями  и  находится по формуле:

где ,  - удельные энергии в сечениях  и  соответственно, м;          - уклон дна канала;  - средний уклон трения.

Удельная энергия  определяется по формуле (7):  

Средний уклон трения  находится по формуле:

где  – средняя скорость воды в канале при средней глубине, м/с;  – средний коэффициент Шези при средней глубине;  – средний гидравлический радиус при средней глубине, м.

Средняя скорость воды в канале  определяется из соотношения (2):

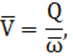
где  - средняя площадь живого сечения при средней глубине.

Средняя площадь живого сечения  находится по формуле:

Средний коэффициент Шези  определяется по формуле Маннинга:

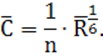
Средний гидравлический радиус  находится по формуле:

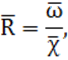
где  - средний смоченный периметр при средней глубине, м.

Средний смоченный периметр  определяется по формуле:

.

Далее все расчеты заносятся в таблицу 6.

Пример расчета таблицы 6 для глубин  и :

1)  площадь живого сечения:

2)  средняя скорость движения воды в канале по формуле (2):

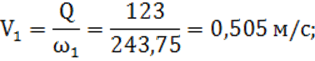
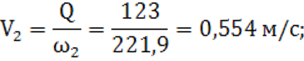
3)  значение скоростного напора :

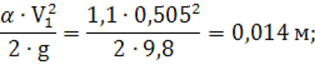
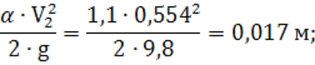
4)  удельная энергия сечения по формуле (7):

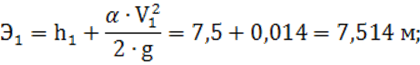
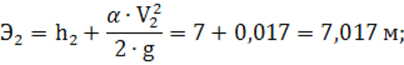
5)  разность удельных энергий сечений:

6)  средняя глубина между поперечными сечениями по формуле (8):

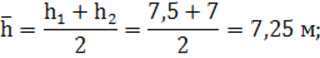
7)  средняя площадь живого сечения:

8)  средний смоченный периметр:

9)  средний гидравлический радиус:

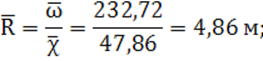
10)  средний коэффициент Шези по формуле Маннинга:

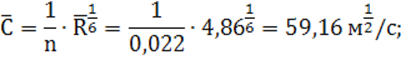
11)  средняя скорость воды в канале при средней глубине:

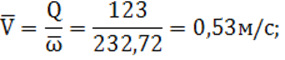
12)  средний уклон трения по формуле (10):

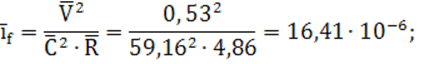
13)  разность уклонов на подводящем участке и среднего уклона трения:

                       

14)  расстояние межу поперечными сечениями канала по формуле (9):

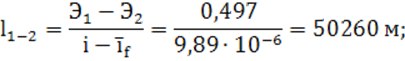
15)  суммарная длина подводящего участка:

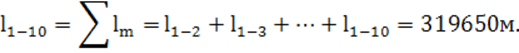
По данным таблицы 6 строится кривая свободной поверхности типа  на подводящем участке канала (рис. 6).

8. Построение кривых свободной поверхности на отводящем участке канала

В зависимости от глубины наполнения, на отводящем участке, могут быть две разные кривые свободной поверхности.

а) Первая кривая свободной поверхности строится методом Чарномского, аналогично как в п. 7. Заполняется таблица 7 (аналогичная таблице 6), в которой задаются значения глубин воды в канале: от глубины воды в сжатом сечении  ( - коэффициент сжатия струи;  - открытие затвора) до

Пример расчета таблицы 7 для глубин  и :

1)  площадь живого сечения:

2)  средняя скорость движения воды в канале по формуле (2):

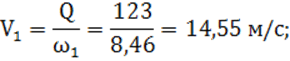
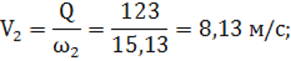
3)  значение скоростного напора :

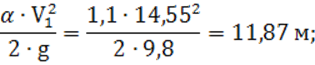
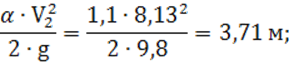
4)  удельная энергия сечения по формуле (7):

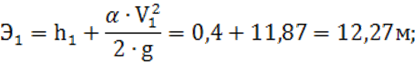
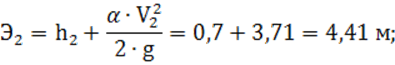
5)  разность удельных энергий сечений:

6)  средняя глубина между поперечными сечениями по формуле (8):

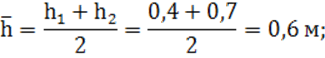
7)  средняя площадь живого сечения:

8)  средний смоченный периметр:

9)  средний гидравлический радиус:

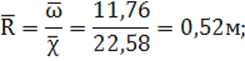
10)  средний коэффициент Шези по формуле Маннинга:

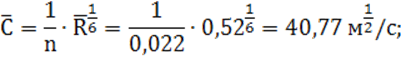
11)  средняя скорость воды в канале при средней глубине:

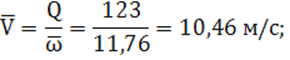
12)  средний уклон трения по формуле (10):

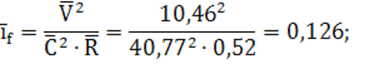
13)  разность уклонов на подводящем участке и среднего уклона трения:

                       

14)  расстояние межу поперечными сечениями канала по формуле (9):

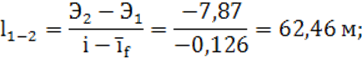
15)  суммарная длина подводящего участка:

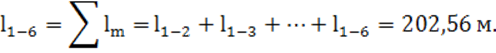
По данным таблицы 7 строится кривая свободной поверхности типа  на отводящем участке канала (рис. 7).

б) Вторая кривая свободной поверхности на отводящем участке канала строится методом Чарномского аналогично первой кривой. Заполняется таблица 8 (аналогичная таблице 7), в которой задаются значения глубин воды в канале: от    до

Пример расчета таблицы 8 для глубин  и :

1)  площадь живого сечения:

2)  средняя скорость движения воды в канале по формуле (2):

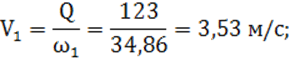
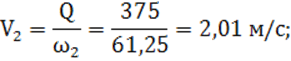
3)  значение скоростного напора :

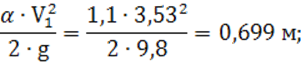
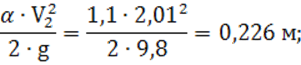
4)  удельная энергия сечения по формуле (7):

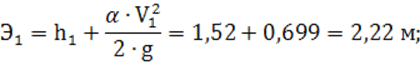
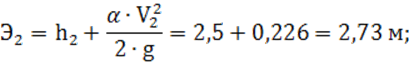
5)  разность удельных энергий сечений:

6)  средняя глубина между поперечными сечениями по формуле (8):

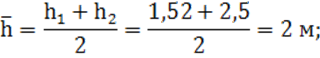
7)  средняя площадь живого сечения:

8)  средний смоченный периметр:

9)  средний гидравлический радиус:

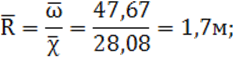
10)  средний коэффициент Шези по формуле Маннинга:

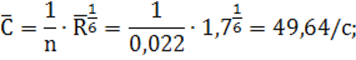
11)  средняя скорость воды в канале при средней глубине:

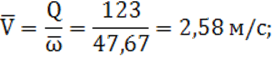
12)  средний уклон трения по формуле (10):

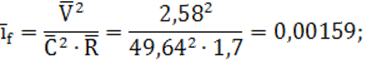
13)  разность уклонов на подводящем участке и среднего уклона трения:

                       

14)  расстояние межу поперечными сечениями канала по формуле (9):

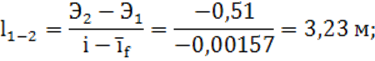
15)  суммарная длина подводящего участка:

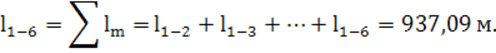
По данным таблицы 8 строится кривая свободной поверхности типа  на отводящем участке канала (рис. 8).

9. Построение графика прыжковой функции

Прыжковая функция имеет следующий вид:

где  - корректив количества движения;  - координата центра тяжести данного живого сечения канала, м.

Координата центра тяжести  определяется по формуле:

Далее для различных значений глубин наполнения канала определяются значения прыжковой функции. Вычисленные данные сводятся в таблицу 9.

Таблица 9.

	м	м2	м	м3
1	0,4	15,2	0,20	991,2
2	2	82,0	0,97	263,3
3	2,2	91,0	1,06	262,5
4	2,5	104,8	1,21	270,1
5	3	128,4	1,44	301,8
6	4	178,4	1,89	422,1
7	8	414,4	3,63	1540,4
8	10	554,0	4,46	2497,2
9	12	708,0	5,27	3750,9
10	14	876,4	6,06	5328,8

Пример расчета строки таблицы 9 для

1)  площадь живого сечения:

2)  координата центра тяжести живого сечения канала по формуле (12):

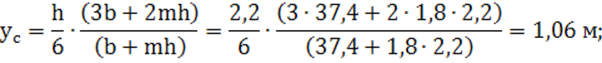
3)  прыжковая функция по формуле (11):

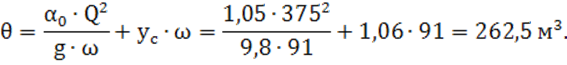
По данным таблицы 9 строится график зависимости прыжковой функции от глубины воды в канале на графике удельной энергии сечения (см. рис. 5).

10. Построение линии сопряженных глубин для кривой типа  и определение местоположения прыжка

Кривая типа  является линией возможных первых сопряженных глубин . Зная первые сопряженные глубины, по графику прыжковой функции ) (см. рис. 5),  определяются вторые сопряженные глубины  . Полученные результаты записываются в таблицу 10.

Таблица 10.

Полученные значения вторых сопряженных глубин откладываются на рис. 8, где изображены кривые свободной поверхности. Построенная кривая является линией вторых сопряженных глубин. В точке пересечении линии вторых сопряженных глубин и линии свободной поверхности типа  находится гидравлический прыжок и соответствующие ему первая и вторая сопряженные глубины:

11. Определение длины гидравлического прыжка и потери энергии в нем

Длина гидравлического прыжка  определяется по эмпирической формуле Бахметьева Б.А.:

Потери энергии в прыжке  определяются с помощью графика удельной энергии сечения  (см. рис. 5):

Схема гидравлического прыжка с напорной линией  представлена на рис. 9.