Модуль накопичення енергії системи енергозабезпечення космічного апарату, страница 11

+ 10,5 ∙ 10³ ∙ 5 ∙ 10^-5 ∙ (0,04 ∙ 2 ∙ 10^-4 + 5 ∙ 5 ∙ 10^-5 ∙ (0.03 – 2 ∙ 10^-4) +

+ 0,03 ∙ 0,04) = 2,9 ∙ 10^-3 кг.

Масса ФЭП на панели определяется как:

М_фэп = М_э ∙ n_э ∙ m_э ∙ n_м ∙ m_м ,                                  (1.39)

где n_э= 6 – число последовательно соединенных элементов в модуле;

m_э = 5 – число параллельно соединенных элементов в модуле;

n_м = 8 – число последовательно соединенных модулей в панели;

m_м = 8 – число параллельно соединенных модулей в панели.

М_фэп = 2,9∙10^-3 ∙ 6 ∙ 5 ∙ 8 ∙ 8 = 5,57 кг,

Определим массу сотопластовой конструкции, состоящей из двух листов стеклотекстолита толщиной 0,6 мм и сотового наполнителя.

Сотовый наполнитель выполняется из листов алюминиевой фольги толщиной 0,1 мм предварительной штамповкой с последующей контактной сваркой по ребрам шестиугольника.

Таким образом, масса сотопластовой конструкции:

М_сот = ,                  (1.40)

где  = 1,8 ∙10³ кг/м³ – плотность текстолита;

 = 1,92 м – длина панели;

 = 1,2 м – ширина панели;

= 0,6 ∙ 10^-3 м – толщина текстолита;

 = 2,6 ∙10³ кг/м³ – плотность алюминиевой фольги;

t_c = 1,6 ∙ 10^-2 м – толщина панели.

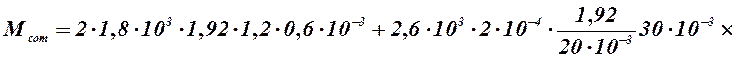
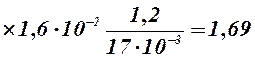кг.

Массу петель определим оценочно по формуле:

,                         (1.41)

где l_п = 8 ∙ 10^{-2 м – размер пластины петли;}

δ_п = 3 ∙ 10^-3 м – толщина пластины;

t_п = 1,6 ∙ 10^-2 м – ширина перегородки;

l_п = 8 ∙ 10^-2 м – длина перегородки;

t_пр = 2 ∙ 10^-2 м – оценочная ширина;

δ_пр = 3 ∙ 10^-3 м – оценочная толщина;

ρ_Ti = 4,507 ∙ 10³ кг/м³ – плотность титана, из которого выполнена петля.

 кг.

М_пан = (5,57 + 1,69 +0,93) ∙ 1,05 = 8,6 кг.

1.5.3.3 Расчет момента инерции панели

Согласно второму закону Ньютона для вращательного движения

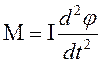,                                                   (1.42)

М-момент инерции панели;

I-осевой момент инерции;

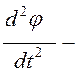ускорение,

t-время раскрытия панели СБ, равное 30 (сек)

;

k-жесткость пружины;

С учетом всего этого преобразуем  1.34.

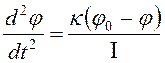.                                        (1.43)

Решением этого дифференциального уравнения является следующее выражение:

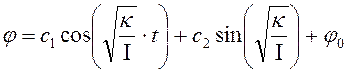.                   (1.44)

Определим константы интегрирования С₁ и С₂ из граничных условий.

При t=0: j=0 и w=j^/=0

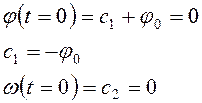.                                            (1.45)

Таким образом, получаем уравнение вращательного движения:

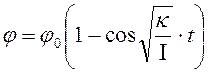.                                           (1.46)

Из этого уравнения определим жесткость пружины:

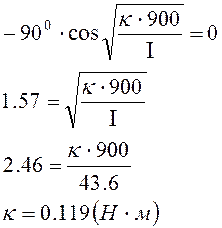  .                                      (1.47)

Находим осевой момент инерции:

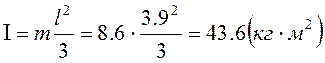.                                 (1.48)

Определяем ускорение по формуле:

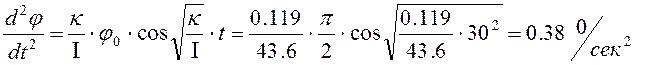
Подставляя числовые значения в выражение 1.34 определяем момент инерции:

.

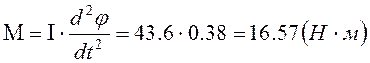Наибольший момент пружины будет равен:

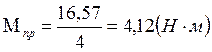.                                 (1.49)

1.5.5Расчет механизма раскрытия

-расчет пружинного двигателя;

Исходные данные:

1.  Наибольший рабочий момент М₂=4,12 (Н×м);

2.  Рабочий угол закручивания пружины (под действием М₂ от состояния при моменте М₁) j₂=360⁰;

3.  Наружный диаметр пружины D_н=38 (мм);

4.  Диаметр проволоки d=5 (мм);

5.  Марка материала 08Х18Н10Т ;

6.   Модуль упругости Е=2×10⁵ (Па);

7.  Допускаемое напряжение на изгиб t_з=250×10⁶(Па);

Определяем:

Максимально допустимый момент:

.                         (1.50)

Предварительный момент:

.                          (1.51)

Индекс пружины:

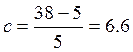.                                                        (1.52)

Из таблицы 202 (2) находим к₁=1,133.

Уточняем значение d по формуле:

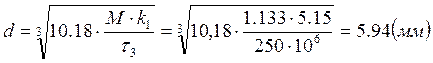.               (1.53)

принимаем d=6(мм).

Рабочие число витков:

.                          (1.54)

Шаг пружины:

.                                                          (1.55)

Угол подъема витков в свободном состоянии пружины:

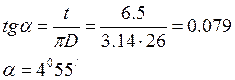.                                                (1.56)

Длина заготовки пружины:

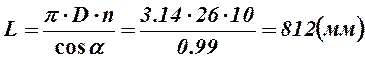.                           (1.57)

Максимальный угол закручивания пружины:

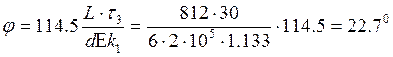             (1.58)

-  расчет редуктора;

Планетарные механизмы служат для передачи вращательного движения цилиндрическими или коническими зубчатыми колесами, в состав которых входят сателлиты (колеса, совершающие сложное движение и имеющие подвижную ось вращения). Подвижное звено, на котором укреплены  оси сателлитов, называется водилом.