Алгоритмы функционирования источников плазмы, страница 9

где р = σ + iω и σ > σ₀ (σ₀ — абсцисса абсолютной сходимости).

Смысл передаточной функции, как явствует из определения, заключается в том, что она представляет собой некий оператор, преобразующий внешнее воздействие на входе в реакцию системы на выходе. Если известно обратное преобразование Лапласа, т. е.

ω(t) =̣˙W(p), то можно записать

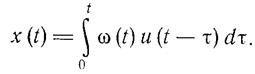                                    (1.2-3.18.)

Интеграл, стоящий в правой части (1.2-3.18.) и определяющий выходной сигнал при нулевых начальных значениях в виде свертки оригинала передаточной функции и внешнего воздействия, называется интегралом Дюамеля.

Все сказанное выше относится к разомкнутым линейным системам. В случае если система является замкнутой или, как говорят, охвачена обратной связью, то передаточная функция определится как

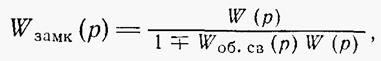                         (1.2-3.19.)

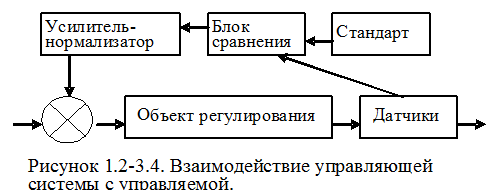
где W_oб.св(р) — передаточная функция элементов обратной связи. Знак «плюс» соответствует отрицательной обратной связи, а знак «минус» - положительной. Формула (1.2-3.19.) легко получается из следующих соображений. Согласно определению передаточной функции

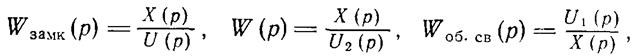          (1.2-3.20.)

но, как видно из рисунка 1.2-3.4.  т. е.,

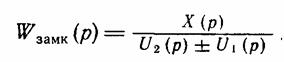                               (1.2-3.21.)

Разделив числитель и знаменатель на U₂(p), получим

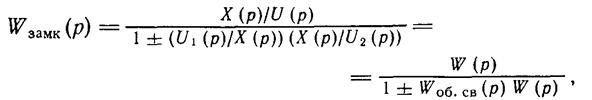          (1.2-3.22.)

Передаточная функция в общем случае является функцией непрерывной и таким же являются входной (тестовый) и выходной (отклик устройства или системы) сигналы. Довольно часто передаточная функция содержит вполне достаточно информации для проведения анализа работоспособности тестируемого устройства (системы). Технически тестирование на основе изучения такой функции не требует существенного усложнения структуры СЭП. Испытательный (тестовый) сигнал генерируется ЭВМ, ею же анализируется отклик тестируемого устройства. Если же по какой-то причине информативности передаточной функции недостаточно для решения вопроса о работоспособности тестируемого устройства, то для проведения тестирования может быть использована т. н. переходная функция.

Переходная функция. Сигнал h(t), получаемый на выходе системы при подаче на его вход единичного скачка u₀(t) (см. приложение), называется переходной функцией системы. Согласно (П4.4.4 из приложения к курсу лекций) u₀(t) =̣˙l/p и, следовательно, по определению (1.2-3.16.) имеем

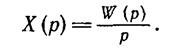                                        (1.2-3.24.)

Переходя от изображения к оригиналу, получим

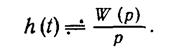                                        (1.2-3.25.)

Между передаточной и переходной функциями существует связь. Из формулы (1.2-3.18.) при u(t) = u₀(t) следует, что

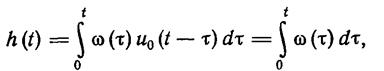                        (1.2-3.26.)

откуда

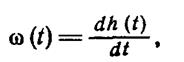                                      (1.2-3.27.)

т. е. оригинал передаточной функции равен производной от переходной функции системы. Не следует забывать, что, как и прежде, система имеет нулевые начальные условия.

Выразим x(t) — реакцию системы на произвольное воздействие u(t) — через переходную функцию h(t). Из (1.2-3.27.) и (1.2-3.18.) имеем

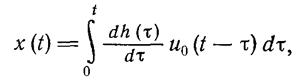                            (1.2-3.28.)

и, производя интегрирование по частям, получим

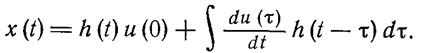                  (1.2-3.29.)

Здесь учтено, что h(0) = 0.

Весовая, или импульсная переходная, функция системы. Прежде чем дать определение весовой функции системы, рассмотрим функцию δ(t), называемую функцией Дирака или дельта-функцией. В теории автоматического управления эту функцию часто называют единичным импульсом. Определим δ(t) следующими соотношениями:

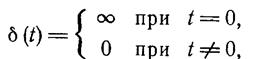                                   (1.2-3.30.)

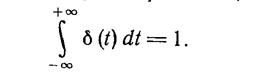                                   (1.2-3.31.)

Очевидно, что δ(t), так же как и u₀(t), является некой математической абстракцией реально существующих сигналов.

Свойства единичного импульса:

1. 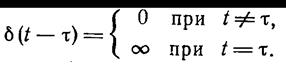                                     (1.2-3.32.)

2. 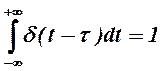                                                          (1.2-3.33.)

3. 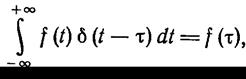                                            (1.2-3.34.)

если f(t) — ограниченная и непрерывная функция. Свойство (1.2-3.34.) дает возможность представить любой сигнал в виде совокупности единичных импульсов:

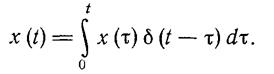                                 (1.2-3.35.)