Анализ физического механизма наращивания толщины пленок, страница 7

Коэффициент  относится к типу кинетических и называется коэффициентом диффузии вещества. Это уравнение справедливо для системы диффундирующих частиц, не взаимодействующих друг с другом и находящихся в хаотическом движении, когда все участки системы характеризуются одинаковыми физическими условиями (температура всюду одинакова, отсутствуют упругие напряжения и т.п.). Подстановка этого уравнения в уравнение для непрерывности среды дает второе уравнение Фика:

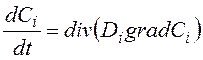.                                            (26)

Для нахождения явного вида коэффициента  необходимо ввести определенные модельные представления о структуре вещества и механизмах элементарных актов процесса диффузии. Коэффициент диффузии  в такого типа теории всегда положителен и диффузионный поток течет из областей с более высокой концентрацией диффундирующего вещества в области с более низкой его концентрацией, т.к. согласно уравнениям (24-25) «движущей силой» диффузии является градиент концентрации.

В макроскопической теории для описания диффузии в кристаллической решетке металлов и сплавов обсуждаются несколько механизмов элементарных актов диффузии: 1) обменный и кольцевой механизмы диффузии; 2) механизмы диффузии по межузлиям: скачком из одного положения равновесия в соседнее, путем вытеснения соседнего атома из нормального положения в решетке в межузлие, путем движения сжатых в некотором направлении атомов; 3) вакансионный механизм; 4)субграничный механизм, в этом случае диффузия осуществляется путем движения атома вдоль дислокационных трубок; 5) релаксационный механизм, диффундирующий атом перемещается в жидкоподобной области, которая в свою очередь, амебообразно движется в кристаллической решетке. В металлах и твердых растворах замещения, где переход атома из узла в междоузлие создает большие искажения и энергетически невыгоден, основным механизмом диффузии является вакансионный. Внедренные атомы обычно перемещаются, диффундируя по междоузлиям.

В работе [9] была исследована  диффузия в крупнокристаллических пленках в системе Pd/Ag со средней плотностью дефектов при температурах диффузионного отжига около 0,5Т_пл. Для того чтобы не происходило существенного изменения структуры образцов во время диффузионного отжига, применялся кратковременный отжиг с использованием миллисекундных лазерных импульсов. В результате эксперимента было установлено, что под воздействием миллисекундных лазерных импульсов в крупнокристаллической системе Pd/Ag наблюдается сравнительно быстрая диффузия. Значения эффективного коэффициента диффузии при 0,62 Т_пл. превышает величины коэффициентов диффузии по решетке в ГЦК металлах при температуре плавления. Наиболее вероятным механизмом такой диффузии является диффузия по движущимся дислокациям.

Перечень ссылок

1.  Технология тонких пленок. Под ред. Л.Майселла, Р.Глэнга. Т.2. М., «Сов. радио», 1977. – 768 с. с ил.

2.  Коропов А.В., Сагалович В.В. Рост островковых структур и критерии образования сплошных пленок. – Харьков: ХФТИ АН УССР, 1988. – 11 с.

3.  Иевлев В.М. Структура островковых пленок металлов // Изв. АН СССР. Сер. Физ. – 1986. Т.50, №8.

4.  Долгов А.С. Неоднородные распределения атомов на поверхности в условиях осаждения извне // Поверхность. Физика, химия, механика. 1988. №7. С. 24.

5.  Долгов А.С., Остроушко В.Н. Кинетика миграции взаимодействующих атомов в кристаллической решетке // Журнал экспериментальной и теоретической физики. 1982. Т. 83. №4. С. 1515.

6.  Осипов А.В. Кинетика конденсации тонких металлических пленок // Металлофизика. 1989. Т. 11, №1.

7.  И.Мак-Даниель. Процессы столкновений в ионизованных газах. – М: Мир, 1967. – 832 с.

8.  Диффузия в металлах и сплавах (труды III всесоюзной конференции) под ред. М.А.Криштала. Тула, 1968. – 448 с.

9.  Бекренев А.Н., Васильев А.Д. Диффузия в кристаллических тонких пленках под действием миллисекундных лазерных импульсов // Физика и химия обработки материалов. 1996. №6. с. 46.