Анализ физического механизма наращивания толщины пленок, страница 3

Рассмотрим процесс послойного наращивания толщины поверхностного покрытия в результате осаждения бомбардирующих атомов.

За основу было взято рассмотренное в [4] взаимодействие частицы с соседними в пределах одной цепи.

В работе рассмотрена модель простой кубической решетки, для которой было получено уравнение равновесной кинетики поверхностного монослоя с учетом эффектов осаждения и испарения:

В случае однородного равновесного распределения при обращении второй производной в нуль мы получаем следующее уравнение:

где  - экстремальная степень заполнения.

Поскольку это уравнение пятой степени, получить корни в общем виде, записанные через коэффициенты, не удалось. Поэтому были рассмотрены некоторые частные случаи. В случае слабого и отталкивательного взаимодействия, когда  неоднородные распределения невозможны, корень уравнения один. При сильном межатомном притяжении, когда  и  получено следующее выражение: 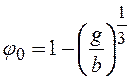. Отсюда видно, что при фиксированном значении фактора экстремальная степень заполнения убывает от максимального значения  до нулевого в точке . При постоянном значении фактора  и с ростом  вероятность  стремится к своему максимальному значению.

Для рассматриваемой модели также были получены уравнения, описывающие поведение системы частиц с изменением времени. Ниже приведено уравнение, определяющее равновесие системы, не зависящее от  и :

Полученная система уравнений для  и , позволяет сделать вывод, что эффекты осаждения и испарения не искажают стационарные равновесные распределения, поскольку они не изменяют соотношения между  и , а лишь влияют на уровни заполнения:

Были получены решения этой системы для  в некоторых частных случаях. При постоянном значении  график функции  представляет собой кривую, выходящую из точки (0,0). В области малых значений функция  возрастает с ростом . С увеличением  на графике появляется зона выпуклости в области малых , при этом большим  соответствуют большие степени заполнения , а значения  для экстремальных точек смещаются вправо, и 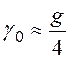. Равным значениям  и  соответствует случай нулевого заполнения позиций. Поэтому, для повышения эффективности осаждения пленок на поверхности рекомендуется, чтобы интенсивность внешней бомбардировки превышала интенсивность испарения в четыре раза.

В процессе осаждения бомбардирующих атомов на поверхность важным этапом является процесс образования и роста островков различных размеров. Форма таких образований будет приближаться к полусферической, а их характеристики в значительной степени будут определяться интенсивностью внешней бомбардировки. Исходя из полученного уравнения изменения объема одного зародыша со временем, были записаны выражения, характеризующие изменение радиуса одного островка, площади его контакта с поверхностью и объема с течением времени:

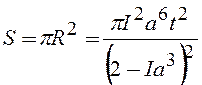.                                                      (7)

С учетом полученного выражения для площади контакта одного островка записано в общем виде уравнение заполнения поверхности сгустками:

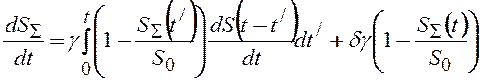                            (8)

Подойти к решению этого уравнения можно путем итераций, что и было проделано для первого приближения:

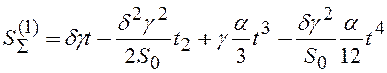                                  (9)

Процессы образования сгустков в моноатомном слое являются отправной точкой для описания неоднородных по толщине пленок. Очевидно, что, как и в моноатомном слое, на процессы, происходящие в неоднородных пленках, влияние будут оказывать как эффекты осаждения и испарения, так и межатомное взаимодействие в пределах одного слоя. Отличие будет заключаться во взаимодействии атома с соседями не только по слою, но также в соседних слоях, как нижележащих, так и вышележащих. Будет распространяться на неоднородные пленки и предположение о том, что с увеличением расстояния между атомами, расположенными в разных слоях, взаимодействия будут ослабевать. В силу этого, рассматривая какой-либо слой атомов, есть смысл учитывать взаимодействия лишь с ближайшими верхними и нижними слоями.