Анализ физического механизма наращивания толщины пленок, страница 5

Нетрудно видеть, что функция, стоящая перед 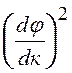является производной от функции, стоящей перед 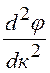. Если обозначить эту функцию

(16)

то уравнение (15) можно переписать в виде:

.

(17)

Функция  называется коэффициентом диффузии и обозначается . Легко увидеть, что в области , т.е. в зоне слабых межатомных взаимодействий, коэффициент диффузии . Общий вид зависимости коэффициента  от степени заполнения  при фиксированных значениях факторов  и  приведен на рисунках (1) и (2). Для определения реальных коэффициентов диффузии, необходимо умножить значение, взятое из графиков, на поправочный коэффициент , где  - шаг кристаллической решетки.

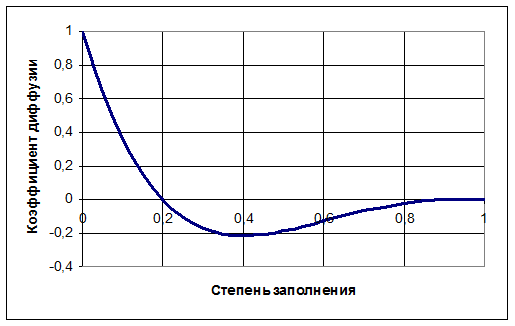
Рисунок 1 Коэффициент диффузии ,

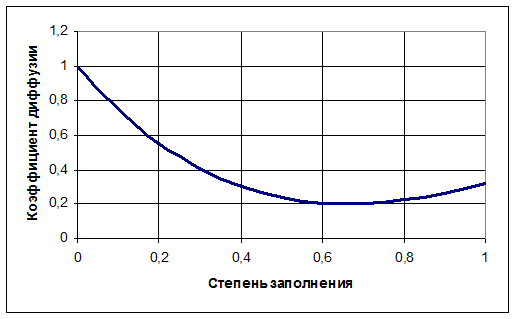
Рисунок 2 Коэффициент диффузии ,

В области сильных взаимодействий между атомами, когда , график функции  с ростом значения  убывает от максимального значения , опускаясь в область отрицательных значений, и затем при  приближается к нулевому уровню. Это говорит о том, что в зоне сильных межатомных взаимодействий диффузия при малых  приводит к образованию равномерных по поверхности заполнений , а в области  - к образованию сгустков.

С ростом значений факторов взаимодействия общий вид графика не меняется, но исчезает область отрицательных значений коэффициента диффузии. Т.е. эффект образования сгустков ослабевает, осаждающиеся атомы заполняют свободные позиции. Можно предположить, что в области высоких степеней заполнения рост коэффициента диффузии ведет к сглаживанию возникающих на поверхности неровностей. Однако это предположение пока не подтверждено экспериментально, что и предлагается осуществить.

Ниже приведены зависимости коэффициента диффузии от факторов межатомных взаимодействий при фиксированном значении степени заполнения .

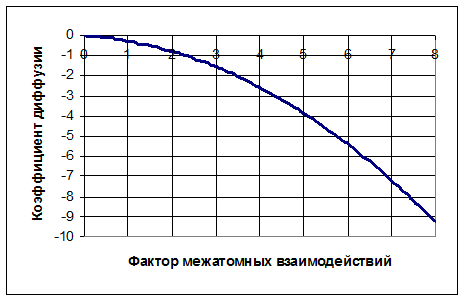
Рисунок 3 Коэффициент диффузии ,

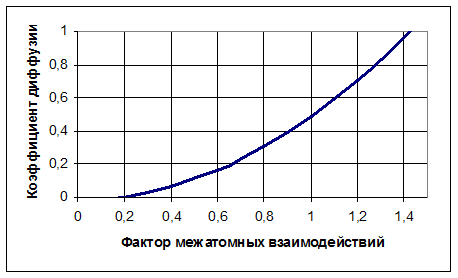
Рисунок 4 Коэффициент диффузии ,

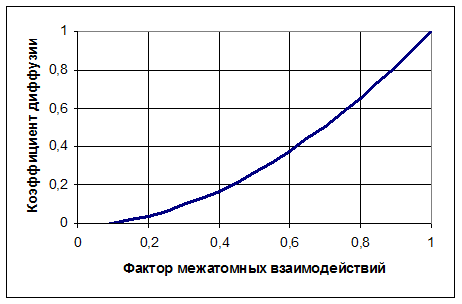
Рисунок 5 Коэффициент диффузии ,

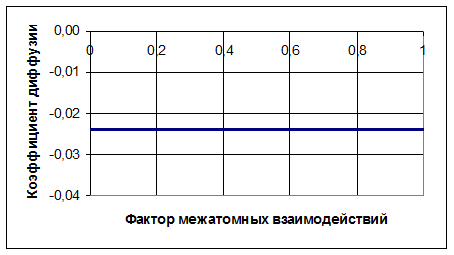
Рисунок 6 Коэффициент диффузии ,

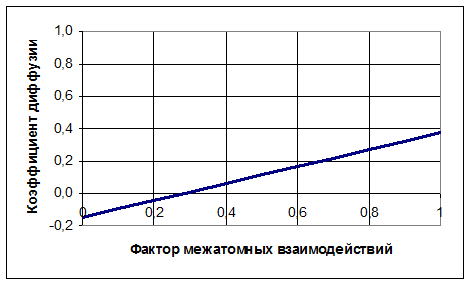
Рисунок 7 Коэффициент диффузии ,

Полученные зависимости позволяют сделать следующие выводы. В области сильных взаимодействий как с атомами в соседних слоях, так и с соседями по слою, процесс диффузии приводит к образованию на поверхности сгустков. С ростом коэффициентов  и  процесс образования сгустков наблюдается лишь в области сильных межатомных взаимодействий при малых степенях заполнения, при этом коэффициент диффузии возрастает с ослабеванием межатомных взаимодействий и переходит в область положительных значений, что свидетельствует о равномерном распределении атомов по поверхности. Следует также отметить, что коэффициент диффузии линейно зависит от фактора межатомных взаимодействий в соседних слоях и квадратично - от фактора взаимодействий в слое.

Приведенная выше система дифференциальных уравнений (17), описывающая поведение системы частиц, представляет собой нелинейную систему, получить решение которой в общем виде довольно затруднительно. Чтобы уйти от нелинейности, выполним линеаризацию уравнений системы, которая заключается в приближенной замене дифференцируемой функции на любом малом участке изменения аргумента на линейную. Добавим, что линеаризация возможна лишь при малых изменениях рассматриваемых величин и основана на отбрасывании величин высшего порядка малости. Таким образом, выполним следующую замену:

,

(18)

где .

На основании вышесказанного, выполняя замену (19), мы получим следующее:

(19)

Эта форма записи не является окончательной и содержит величины высшего порядка малости. Однако, перед тем как доводить линеаризацию до конца, следует отметить, что в уравнении для верхнего слоя будет присутствовать слагаемое, содержащее фактор внешней бомбардировки. В этом случае уравнение верхнего слоя будет единственным, содержащим такое слагаемое.

В ходе последовательных преобразований, отбрасывая величины высших порядков малости, мы получили следующую систему линейных дифференциальных уравнений из N неизвестных: