Анализ физического механизма наращивания толщины пленок, страница 4

Рассматривалась неоднородная по толщине пленку, состоящая из N слоев. Слои нумеруются начиная с верхнего, таким образом, что самый верхний слой является первым.

Согласно уравнению для неоднородных пленок [5] в допущении однородности вдоль поверхности пленки можно записать:

где  - факторы, пропорциональные вероятностям выхода изолированного атома из -го слоя и интенсивности внешней бомбардировки соответственно. В записанном выражении первое слагаемое соответствует вероятности того, что бомбардирующий атом достигнет -го слоя и займет в нем вакантную позицию. Очевидно, что больше всего шансов у атомов извне занять вакантные позиции в самом верхнем слое. Поэтому первое слагаемое в уравнении для первого слоя будет наибольшим, и с удалением от верхнего слоя будет уменьшаться. Например, чтобы атом смог достигнуть вакантной позиции в третьем слое, свободными должны оказаться позиции во втором и в первом слоях одновременно над требуемой позицией. Таким образом, очевидно, что эффект осаждения оказывает влияние в основном на верхние слои, в нижних слоях это влияние оказывается настолько малым, что им можно пренебрегать.

Второе слагаемое в уравнении (10) показывает ту вероятность, с которой атом может выйти из рассматриваемого слоя при условии, что в этом слое у него может быть разное количество соседей (рассматривается простая кубическая решетка), а также различное количество соседей и в различных комбинациях в соседних слоях.

Здесь фактор  описывает межатомные взаимодействия в пределах слоя, фактор  - между соседними слоями. С точки зрения физики нет причин различать между собой эти величины, т.е. случай, когда  является довольно реалистическим.

Третье слагаемое в выражении для 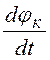 соответствует той вероятности, с которой атом из вышележащего, -го слоя, может занять позицию в рассматриваемом -ом слое, также при наличии различного количества соседей как в самом -ом слое, так и в лежащем над ним -ом слое.

Последнее слагаемое показывает вероятность, аналогичную предыдущей, однако оно относится не к вышележащему, а к нижележащему слою.

Особого внимания заслуживает уравнение (10) для верхнего слоя атомов:

Как уже отмечалось выше, влияние фактора осаждения в этом случае будет максимальным. Еще одной особенностью этого уравнения является то, что, описывая самый верхний слой пленки, оно не содержит слагаемое, соответствующее вышележащему слою. Аналогичным свойством будет обладать уравнение для самого нижнего, -го слоя: оно не будет содержать слагаемое, соответствующее нижележащему слою.

В результате мы получили систему из  дифференциальных уравнений, каждое из которых, кроме первого и последнего, содержит  неизвестных.

Если мы рассмотрим систему уравнений (10) в области слабых межатомных взаимодействий, когда , общий вид уравнений примет более простую форму, при этом каждое уравнение будет содержать  неизвестных:

В этом случае уравнение для верхнего слоя примет следующую форму:

Для полученной упрощенной системы уравнений можно найти решения, однако они будут довольно громоздкими. В итоге мы получили зависимость средних степеней заполнения  от времени с учетом влияния эффектов осаждения и испарения. Имея решение этой системы, можно будет однозначно говорить о распределениях атомов по слоям с течением времени. Другими словами, решив систему (12), мы получим ряд выражений, описывающих рост неоднородных по толщине пленок, а также степень их дефектности.

Анализировать уравнения (10) следует на основе перехода к уравнениям сплошной среды (континуальное приближение):

На основании полученной системы уравнений в терминах сплошной среды, выполняя последовательные преобразования и учитывая слагаемые до второго порядка включительно, была получена система дифференциальных уравнений второго порядка в следующем виде: