Статистические методы исследования качества изделий при механической обработке. Основные термины, применяемые при оценке качества изделий с использованием математической статистики, страница 4

2. Распределение погрешности   эксцентриситета,   биения при закреплении в многокулачковых и цанговых патронах, разностенности втулок и др.   подчиняются   закону Релея   (рис. 2.10);   математическое ожидание:  

М(x)= а = 1,92s; поле рассеяния: w= 5,252s.

3. При обработке заготовок с точностью 7–го и 8–го (иногда 6–го) квалитетов, распределение размеров в большинстве случаев подчиняется закону Симпсона (треугольника, рис. 2.8):  математическое ожидание 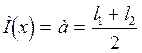;  поле рассеяния .  

4. Распределение случайных погрешностей характеризуется законом Гаусса  (нормального распределения, рис. 2.5). Такому закону соответствуют размеры деталей в партии, изготовленные на настроенном станке при хорошей отладке и стабильности техпроцесса, когда влияние закономерно - изменяющихся факторов проявляется незначительно, а также обусловленных влиянием деформации системы под действием сил резания и сил закрепления, погрешностью установки и др.

Кривая симметрична относительно центра группирования, а ее ветви простираются в бесконечность, приближаясь к оси x. Она имеет перегибы в точках -s и +s. Наибольшая плотность вероятности в центре группирования: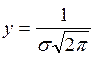. Площадь кривой нормального распределения от а до X_а:

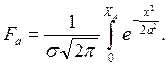
Для табулирования получено уравнение:

По этому уравнению в приложении 1 составлены таблицы Ф(z) при различных значениях безразмерного квантиля распределения (коэффициента)  z  (dx=sdz). Вся площадь под кривой нормального распределения F=1. 

Для практических целей нет необходимости использовать бесконечные пределы: в интервале  x= ±0,7s (z= ±0,7) 50%F,  x= ±3s (99,73%F). Поэтому считают, что все поле рассеивания параметра лежит в интервале ± 3s при ошибке 0,27% . Тогда все поле рассеивания равно: w_p = 6s.

АНАЛИТИЧЕСКИЕ МЕТОДЫ ОПРЕДЕЛЕНИЯ ПОГРЕШНОСТЕЙ

                 Виды погрешностей. Законы распределения.

Погрешности установки и обработки различаются по характеру возникновения при обработке партии деталей: систематические постоянные- w_П.: Например неперпендикулярность оси отверстия при сверлении к базовой плоскости детали вследствие неперпендикулярности оси шпинделя сверлильного станка к плоскости его стола; погрешность межосевого расстояния отверстий в детали из-за неправильно выполненного расстояния между осями кондукторных втулок; погрешность настройки станка на размер; неточность размерного режущего инструмента (РИ);

закономерно изменяющиеся- w_зи. Они изменяют свою величину или знак при переходе от одной обрабатываемой заготовки к следующей. Например, из-за износа инструмента;

случайные погрешности. w_сл.  Для различных заготовок партии погрешности имеют различное значение и ее появление не подчиняется никакой видимой закономерности. Они возникают в результате действия большого количества не связанных между собой факторов.

Расчетно - аналитический метод определения суммарных погрешностей

Последовательность определения суммарной погрешности:

изучение условий выполнения операции;

выявление перечня факторов, обуславливающих появление первичных погр. обработки и установки;

определение значений первичных погрешностей; установление законов распределения для каждой из первичных погрешностей: а) случайные погр., подчиняющиеся закону нормального распределения, складываются по правилу квадратичного корня;

б) случайные погрешности, подчиняющиеся другим законам и закономерно- изменяющиеся погрешности суммируются с учетом закона их распределения;

в) систематические постоянные погрешности складываются алгебраически с учетом их знака, а для генеральной совокупности - арифметически.

непосредственное суммирование первичных погрешностей. v_ГС для генеральной совокупности:

, где Sw_in  - cумма систематических погрешностей;  К_i и К_S - коэффициенты относительного рассеивания соответствующих погрешностей и их сумма: закон Гаусса - К_iг =1; закон Симпсона - К_iс = 1,22; закон равной вероятности - К_ip =1,73.

В пределах отдельно взятой партии: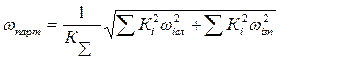

Статистический контроль стабильности и анализ точности изготовления изделий в серийном производстве

Статистический метод оценки точности применим в условиях производства большого числа одинаковых деталей, обработанных как на предварительно настроенных станках, так и методом пробных рабочих ходов с использованием кривых распределения, которые строят описанным выше способом.