Статистические методы исследования качества изделий при механической обработке. Основные термины, применяемые при оценке качества изделий с использованием математической статистики, страница 3

Действует при рассеянии размеров, зависящих от переменных систематических погрешностей (например, износ режущего инструмента). Если  размер заготовки изменяется в этом случае по прямой, то распределение размеров в интервале  ab  подчиняется закону равной вероятности (рис. 2.9).

Статистические характеристики определяют по формулам

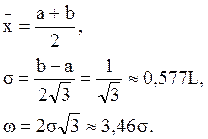                     (2.7)

Закон равной  вероятности распространяется на распределение размеров заготовок повышенной точности (5...6 квалитеты и выше) при обработке пробными ходами.

Закон равной вероятности (Размерный износ, температурные деформации)

Закон эксцентриситета  (закон Релея)

Этому закону подчиняются распределения эксцентриситета, биения, разностенности, непараллельности, неперпендикулярности, овальности, конусообразности и других существенно положительных величин, характеризующих их абсолютными значениями (без учета знака).

Например, после обработки втулки 1 на цилиндрической оправке 2 вследствие    наличия    между    ними    зазора    образуется      экцентриситет. При обработке  партии  деталей  экцентриситет имеет  распределение,  подчиняющееся закону Релея. 

Закон экцентриситета (Релея) (эксцентриситет,   биение при закреплении в многокулачковых и цанговых патронах, разностенности втулок и др.)

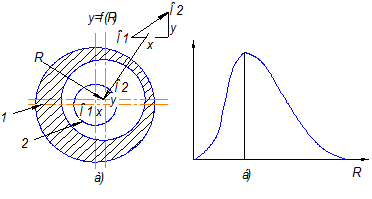
Распределение  Релея   формируется тогда, когда случайная величина R является радиусом-вектором при двумерном гауссовском распределении

                                       R=                              (2.8)

каждая из которых ( x  и y ) подчиняется закону Гаусса с параметрами

   

Виды погрешностей. Законы распределения

Большое число технологических факторов, влияющих на точность исполнения размеров, формы и относительного положения поверхностей, приводит к появлению бракованных изделий. Поэтому необходимо иметь представление о поведении параметров по результатам  изготовления некоторой партии изделий и правильно их анализировать. Для этого в практике широко используют аналитические методы исследования технологических процессов.

Погрешности установки и обработки при механической обработке заготовок различаются по характеру возникновения при обработке партии деталей:

систематические постоянные – w_П. 

Например, отклонение от перпендикулярности оси отверстия при сверлении к базовой плоскости детали вследствие неперпендикулярности оси шпинделя сверлильного станка к плоскости его стола; погрешность межосевого расстояния отверстий в детали из-за неправильно выполненного расстояния между осями кондукторных втулок; погрешность настройки станка на размер; неточность размерного режущего инструмента (РИ);

закономерно изменяющиеся – w_зи.

Этот вид погрешности изготовления деталей изменяет свою величину или знак при переходе от одной обрабатываемой заготовки к следующей. Например, из-за износа инструмента;

случайные погрешности – w_сл.  

Для различных заготовок партии погрешность изготовления заготовки различна и ее появление не подчиняется никакой видимой закономерности. Эта погрешность возникает в результате действия большого количества не связанных между собой факторов.

Наличие случайных и закономерно - изменяющихся погрешностей обуславливает рассеивание размеров или других параметров. Это значит, что одноименные размеры заготовок, обработанные при внешне стабильных условиях (на одном станке, одной настройке, в одном кондукторе и т.д.), различаются между собой.

Закон распределения закономерно - изменяющейся погрешности зависит от характера действия причины, вызывающей эти погрешности.

1. Размерный износ изменяется по закону прямой x=ct , а это значит, что распределение этой погрешности будет по закону равной вероятности (см. рис. 2.9). К этому же закону относится поведение погрешности от температурных деформаций системы СПИД.

Если на точность влияет только размерный износ инструмента или температурные деформации системы, то уравнение равной вероятности будет характеризовать распределение размеров всех заготовок партии (уравнение плотности вероятности ; математическое ожидание ; поле рассеивания  ).