Статистические методы исследования качества изделий при механической обработке. Основные термины, применяемые при оценке качества изделий с использованием математической статистики, страница 2

изменение положения исходной заготовки в приспособлении, связанное с погрешностями базирования и закрепления;

неточности установки положения суппортов по упорам и лимбам;

колебания температурного режима обработки и упругих отжатий  элементов технологической системы под влиянием нестабильных сил резания и т.п.

В технологии машиностроения практическое применение имеют следующие математические законы.

     Закон нормального распределения  (закон Гаусса)

Этому закону подчиняются размеры заготовок, обработанные на настроенных станках. Размеры получаются в результате действия большого числа взаимно независимых случайных величин, зависящих от качества системы СПИЗ. Уравнение кривой нормального распределения имеет вид:

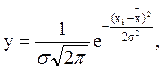                                (2.1)

где s -среднее квадратичное отклонение.

Среднее квадратичное отклонение определяется по формуле

,          (2.2)

где x_i - текущий действительный размер;  - среднее арифметическое значение действительных размеров заготовок:

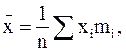                                   (2.3)

где  m_i - частота появления события; n - количество заготовок в партии.

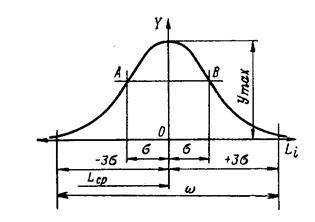
На рис. 2.5  показана кривая нормального распределения, симметричная относительно оси ординат. При   кривая  нормального распределения имеет максимальное значение:

.                                 (2.4)

На расстоянии   ±s от  y_max   кривая имеет точки перегиба

       y₁=y₂=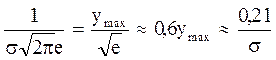                             (2.5)

Кривая асимптотически приближается к оси абсцисс. 

На  расстоянии ±3s в пределах кривой оказывается  99,73%  площади  F:  F₁ = 0,9973F.  Если принять, что все размеры находятся  в пределах  площади F,  то  погрешность  определения будет равна 0,27%.

При увеличении  s, поле рассеяния возрастает, кривая рассеяния параметров становится более пологой и низкой. Это свидетельствует о меньшей точности изготовления. Поле рассеяния размеров находится в диапазоне  w = 6s.

Размер каждой заготовки  в партии является случайной  величиной  и имеет значения в границах определенного интервала.  Измеренные значения истинных размеров заготовок разбивают на интервалы (разность между наибольшим и наименьшим размерами в пределах одного интервала). Размер интервала должен быть меньше погрешности измерительного устройства, тем самым компенсируются погрешности измерения. Распределение размеров  заготовок представляют в виде таблицы (табл. 2.14), в которой приняты следующие обозначения: n - общее количество измерений, m- частота появления размера в интервале, m/n- доля частоты появления размера к общему количеству измерений (m = 100 ,  ).

Кривая нормального распределения (закон Гаусса) (размеры деталей, обработанные на настроенных станках; масса заготовок и деталей машин, твердость, механические свойства материалов, высота микронеровностей на обработанных поверхностях, погрешности измерений)

                          

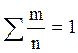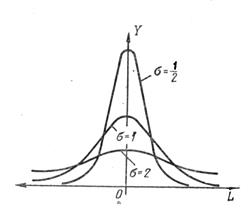
Влияние величины  s  на форму кривой Гаусса

Распределение размеров заготовок

№ интервала	Интервал	Частота, m	Доля частоты, m/n
1 2 3 4 5 6 7	20,00-20,05 20,05-20,10 20,10-20,15 20,15-20,20 20,20-20,25 20,25-20,30 20,30-20,35	2 11 19 28 22 15 3	0,02 0,11 0,19 0,28 0,22 0,15 0,03

По результатам измерения строится гистограмма (рис. 2.7). Ломаную кривую 1 называют эмпирической кривой распределения. При увеличении количества интервалов кривая 1 приближается к плавной кривой, называемой кривой  распределения.

 

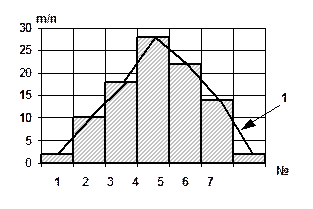
Гистограмма распределения размеров по интервалам

 Закон  Симпсона  (равнобедренного треугольника)

При обработке заготовок с точностью 7,8 и в некоторых  случаях 6-го квалитета     распределение    их   размеров   подчиняется   закону   Симпсона

(рис. 2.8) с полем рассеянияl = w = 2                     (2.6)

Закон треугольника (Симпсона)

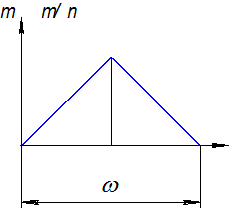
Закон равной вероятности