Функционирование криптографических систем при конкретных параметрах, страница 14

4.3. Криптосистеме Эль - Гамаля.

4.3.1. Проектирование системы.

Генерация ключей:

k(n) = 101111010000101111₂

p= p((₁[k(n)]₃)₁₀) = p (5)

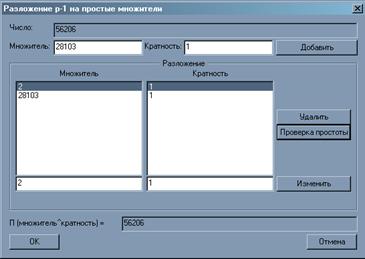
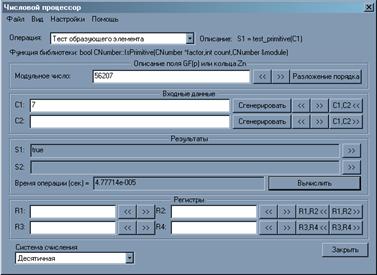
p = 56207

Вычисляем  образующий элемент α  мультипликативной группы Z_p^* .

·  Разлагаем число p – 1 на простые множители.

·  В числовом процессоре,  при помощи операции «Тест образующего элемента находим a »

α = 7

Выбираем случайное a, 1<a£p-2.

a = 67

Вычисляем β = α  ^a mod p.

β = 7⁶⁷ mod 56207 = 4034

β = 4034

Открытым ключом объявляем тройку чисел (p, α, β).

К_о = (56207, 7, 4034)

В качестве секретного ключа сохраняет число a.

4.3.2. Тестирование.

Шифровать и расшифровать сообщения m =  ₁[k(n)]₄.)

Шифрование:

Представляем сообщение, как число m из интервала [0, p-1].

k(n) = 101111010000101111₂

m = ₁[k(n)]₄ = 1011₂ = 11₁₀ (по условию задания)

m = 11

Выбираем случайно число k, 0<k<p-1.

k = 23

Вычисляем d = α ^k mod p.

d = 7²³ mod 56207 = 25116

d = 25116

Вычисляем e = m β ^k mod p.

e = 52492

Посылаем шифртекст (d, e).

 с = (25116, 52492)

Расшифрование:

Вычисляет сообщение m = (d^-a)e mod p.

m’ = 52492*(25116⁶⁷)^-1 mod 56207= 11

m’ = 11

Убеждаемся, что m’ = m = 11

4.3.3. Поблочное шифрование и расшифрование большого текста m.

m = 9100 9200 9300 9400 9500

Разбираем открытый тест  m на блоки, позволяющие шифрование полученной криптосистемой. (m = [0, p-1]). m = m₁,…m_t