Функционирование криптографических систем при конкретных параметрах, страница 11

q= p((₁[k(n)]₆)₁₀+4) = q (51)

p(47) = 5261545651643092682066113878001567

q(51) = 28152899513074107153559896243858108887

n=p×q.

n = 148127766014160009790321680247818844317430111080457586551679959442625929

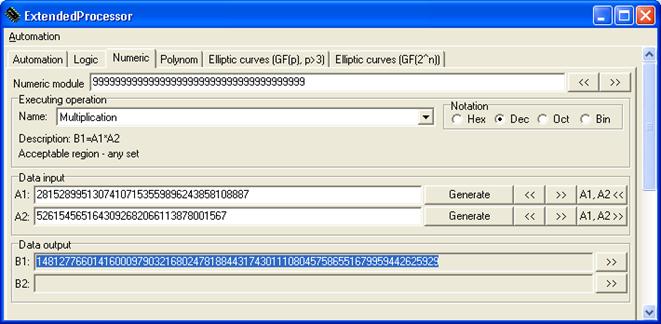
4.2.2. Тестирование.

Возьмем сообщение m=k(n), зашифруем и расшифруем.

Шифрование:

m = k (n) =  101111010000101111₂ = 9154₁₀

c = m² mod n = 9154² mod n = 83795716

Расшифрование:

Находим квадратный корень из числа с по модулю числа n:

Вычисляем квадратные корни  r и - r числа c по модулю p.

sqrt (c, mod p) = (9154, 5261545651643092682066113877992413)

 r = 9154

-r = 5261545651643092682066113877992413

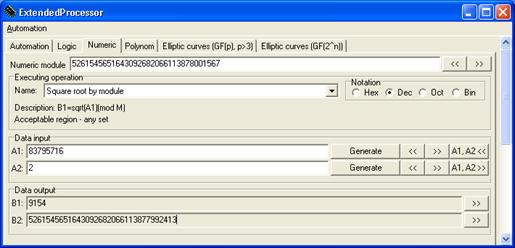
Вычисляем квадратные корни s и - s числа c по модулю q.

sqrt (c, mod q) = (28152899513074107153559896243858099733, 9154)

 s = 28152899513074107153559896243858099733

-s = 9154

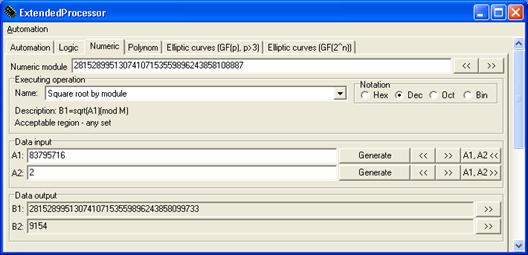
По расширенному алгоритму Евклида вычисляем числа a и b (ap +bq = 1)

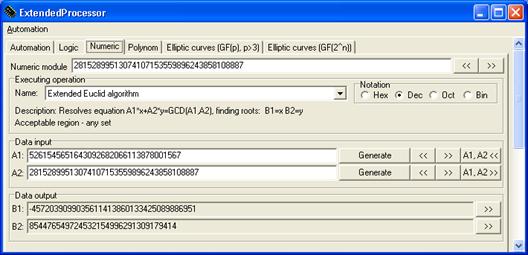
a = q -4572039099035611413860133425089886951 = 23580860414038495739699762818768221936

b = 854476549724532154996291309179414

Вычисляем x = spa + rqb mod n и y = spc-rqb mod n.

p*a = 124071773573486985374889983909896255453155964315646560215690637611773712

q*b = 24055992440673024415431696337922588864274146764811026335989321830852218

spa = 3492980173823262626249237427206789863720498848670654900802290846286417020880417823769121088460226795923618896

rqb = 220208554801920865498861748277343378463565539485080135079646252039621203572

x = spa + rqb mod n

x  = 33261243744021891097141177921332771411358727959865341147984656315511073

-x = 114866522270138118693180502326486072906071383120592245403695303127114856

y = spc-rqb mod n

y = 148127766014160009790321680247818844317430111080457586551679959442616775