Метрические и линейные нормированные пространства
Ниже везде R – множество действительных чисел
Ответить на следующие вопросы:
(a) Является ли метрическим пространством заданное множество M с определенной на нем функцией d: M´M ® M ?
(b) Будет ли (M, d) полным метрическим пространством?
1. M = R , d(x,y) = | x3 – y3 |
2. M = R2 , d((x1,y1), (x2 ,y2 ) ) = | x1 – x2| + |y1 – y2|
3. M = R , d(x,y) = | ex – ey |
4. M = R , d(x,y) = min ( 1, |x-y| )
5. M = R ,
d(x,y)=|
![]() –
– ![]() |
|
6. M – множество прямых в декартовой плоскости, не
проходящих через начало координат; для прямых l1:
x cos a1 + y sin a1 – p1 = 0 и l2: x cos a2 + y sin a2 – p2 = 0 значения d определяются по формуле 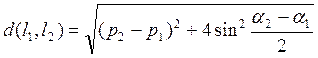
7. M = {x Î R : x ³ 0} , d(x,y)= ![]()
8. M – множество прямых в декартовой плоскости, не
проходящих через начало координат; для прямых l1:
x cos a1 + y sin a1 – p1 = 0 и l2: x cos a2 + y sin a2 – p2 = 0 значения d определяются по формуле ![]()
9. M = R , d(x,y)= ![]()
10. M
– множество прямых l: x cos a + y sin a – p = 0
в декартовой плоскости, для которых 0£a<p
; для прямых l1: x cos a1 + y sin a1 – p1
= 0 и l2: x cos a2 + y sin a2 – p2
= 0 значения d определяются
по формуле ![]()
11. M = {x Î R : x ³ 0}, d(x,y)= ![]()
12. M = R , d(x,y)=|arctg(x–y)|
13. M = R , ![]()
14. M = R , d(x,y)=| arctg x – arctg y|
15. M – множество замкнутых отрезков [x,y] на прямой, d([x1,y1], [x2 ,y2 ] ) = | x1 – x2| + |y1 – y2|
16. M = {x Î R : x ³ 0}, d(x,y) = |x2 – y2|
17. M – множество замкнутых отрезков [x,y] на прямой, d([x1,y1], [x2 ,y2 ] ) = | [x1,y1] | + |[x2 , y2]| – 2|[x1,y1] Ç [x2 ,y2 ]| , где |[x,y]|=|x – y|
18. M ={x Î R : x > 0} d(x,y)= ![]()
19. M = N –
множество неотрицательных целых чисел, 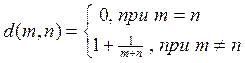 .
.
20. M = R , 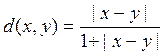
21. M
– множество рациональных чисел, фиксируем простое число p,
определим d(x, y) = p-k , если x – y = pk![]() , где m и n – целые
числа, взаимно простые с числом p.
, где m и n – целые
числа, взаимно простые с числом p.
Построить оператор для решения заданного уравнения. Доказать, что он является сжимающим. Построить последовательные решения интегрального уравнения и оценить точность
1.
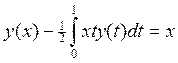
2.
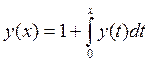 , y0(x)=0 exp(x)
, y0(x)=0 exp(x)
3.
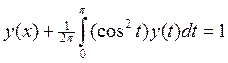
4.
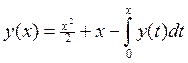 , y0(x) = 1 y(x)=x
, y0(x) = 1 y(x)=x
5.
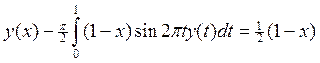
6.
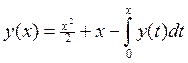 ,
, ![]() y(x)=x
y(x)=x
7.
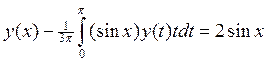
8.
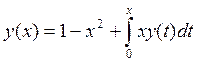 , y0(x)=1-x2
. y(x)=1
, y0(x)=1-x2
. y(x)=1
9.
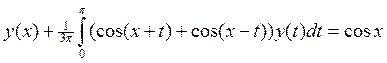
10.
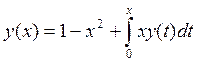 , y0(x)=1. y(x)=1
, y0(x)=1. y(x)=1
11.
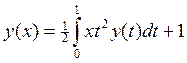 (4/21)x+1
(4/21)x+1
12.
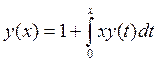 , y0(x)=1. y(x)=
, y0(x)=1. y(x)=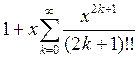
13.
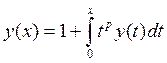 , y0(x)=1
; p=0, 1, 2, ××× y(x)=
, y0(x)=1
; p=0, 1, 2, ××× y(x)=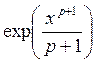
14.
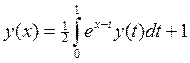 exp(x)
– exp(x–1)+1
exp(x)
– exp(x–1)+1
15.
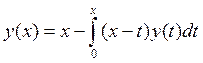 , y0(x)=0. y(x)=sin
x
, y0(x)=0. y(x)=sin
x
16.
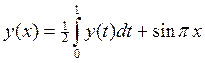
17.
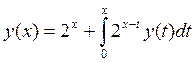 , y0(x)=0 y(x)=(2e)x
, y0(x)=0 y(x)=(2e)x
18. 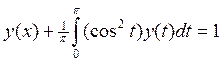 2/3
2/3
19. 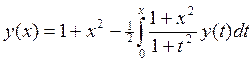 , y0(x)=0 y(x)=
, y0(x)=0 y(x)=![]()
20. 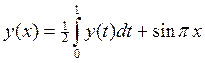
Пусть (M,d) – метрическое пространство, E – его подмножество. Точкой прикосновения множества E называется точка xÎM, в любой окрестности которой существует по крайней мере одна точка из E.
Точка xÎE называется предельной точкой множества E, если любая окрестность точки x содержит по крайней мере одну точку из E, не равную x. (Предельная точка множества E не обязана принадлежать E .)
Множество всех предельных точек подмножества E метрического пространства называется производным множеством E’ .
Подмножество EÍM называется открытым, если каждая его точка является внутренней, т.е. содержится в E вместе с некоторой окрестностью B(x,e).
Подмножество, содержащее все свои точки прикосновения, называются замкнутыми.
Точка xÎE называется граничной точкой множества E, если любая ее окрестность содержит как точки, принадлежащие E, так и точки, не принадлежащие E.
Отображение f : M ®M’ метрических пространств называется непрерывным в точке xÎM, если
(" e > 0) ( $ d > 0) d(x,x’) < d Þ d’(f(x), f(x’)) < e
Отображение f : M ®M’ метрических пространств называется непрерывным, если оно непрерывно в каждой точке xÎM.
Непрерывная биекция между метрическими пространствами, имеющая непрерывное обратное отображение, называется гомеоморфизмом.
1. Дано некоторое множество точек E на плоскости. Известно, что нижняя грань расстояний между различными точками из E больше нуля. Доказать, что множество E не имеет предельных точек.
2. Построить множество, для которого производное множество не пусто, а второе производное множество пусто.
3. Справедливо ли утверждение: Производное множество от пересечения двух множеств AÇB равно персечению производных множеств от каждого множества в отдельности?
4. Доказать: Если предельная точка не принадлежит множеству, то она является его граничной точкой.
5. Доказать, что пересечение последовательности плотных открытых подмножеств прямой является плотным подмножеством.
6. Доказать утверждение: Если в метрическом пространстве любая последовательность точек содержит фундаментальную подпоследовательность, то это метрическое пространство сепарабельно.
7.
Пусть B[x,r] = {x’: d(x’,x)£ r }. Доказать diam B[x,r] £
2r и ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.