Метрические и линейные нормированные пространства, страница 2

8.  Доказать утверждение: Точка x является точкой прикосновения (соотв. предельной точкой) множества M в метрическом пространстве X тогда и только тогда, когда d(x,M)=0 (соответственно d(x, M\{x})=0).

9.  Доказать утверждение: Замыкание нигде не плотного подмножества метрического пространства нигде не плотно.

10.  Доказать утверждение: Пересечение всех содержащих множество M замкнутых подмножеств метрического пространства совпадает с .

11.  Пусть f: M®R – непрерывная функция на метрическом пространстве. Доказать, что подмножество {x: f(x)³0} замкнуто в M.

12.  Доказать, что отображение между метрическими пространствами непрерывно тогда и только тогда, когда оно сходящиеся последовательности переводит в сходящиеся и  перестановочно с пределами.

13.  Пусть E – произвольное подмножество метрического пространства (M, d). Доказать непрерывность функции f(x)=d(E,x)=inf {d(e,x): eÎE}.

14.  Доказать: Для любых точки xÎM, числа e>0 и точки x’ÎB(x, e) существует число e’ >0, такие, что B(x’, e’)Í B(x, e).

15.  Доказать, что топология метрического пространства удовлетворяет аксиоме отделимости Хаусдорфа.

16.  Доказать, что подмножество E метрического пространства замкнуто тогда и только тогда, когда для любого xÏE верно d(x,E)>0.

17.  Доказать, что подмножество E метрического пространства M замкнуто тогда и только тогда, когда для любой сходящейся в M последовательности x_nÎE ее предел lim x_n тоже принадлежит E.

18.  Доказать, что отображение метрических пространств непрерывно, если и только если прообраз каждого открытого множества является открытым.

19.  Пусть (M,d) – метрическое пространство. Доказать, что M с метрикой d*(x,y)=max(1,d(x,y)) гомеоморфно (M,d). Если (M,d) полно, то (M,d*) полно.

20.  Доказать, что отображение метрических пространств непрерывно, если и только если прообраз каждого замкнутого множества является замкнутым.

21.  Доказать, что метрическое пространство рациональных чисел не гомеоморфно никакому полному метрическому пространству.

Задача 4

Убедиться в том, что в следующих случаях выполняется аксиома нормы. Что означает сходимость в каждом из перечисленных ниже случаев?

Варианты

1.  Пространство c сходящихся   последовательностей x=(x_k)_k³1 , состоящих из чисел из R , с нормой  ||x|| = sup { |x_k| : k ≥1}.

2.  Пространство C^k[a,b], состоящее из k раз непрерывно дифференцируемых на [a,b] функций с нормой  ||x|| = .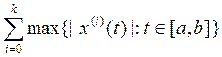

3.  Пространство M[a,b] всех ограниченных на [a,b] функций с нормой  ||x|| = .

4.  Пространство K непрерывных на вещественной прямой финитных функций (равных нулю вне некоторого интервала, своего для каждой функции)  с нормой  ||x|| =

5.  Пространство C_p[a,b] непрерывных на [a,b] функций с нормой  ||x|| = ,  .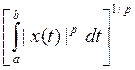

6.  Пространство V[a,b]  функций с ограниченной на [a,b] вариацией с нормой ||x|| = 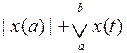. Здесь под функцией с ограниченной вариацией понимается функция на [a,b], для которой существует постоянная c такая, что для любого разбиения отрезка a=t₀<t₁<…<t_n=b  выполняется неравенство 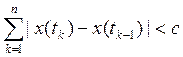.  Для такой функции ее полной вариацией называется число ,  где верхняя грань берется по всевозможным конечным разбиениям отрезка [a,b].

7.  Пространство E^m столбцов x=(x_k), состоящих из m чисел из R , с нормой ||x|| =.

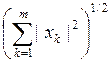8.  Пространство c^m столбцов x=(x_k), состоящих из m чисел из R , с нормой ||x|| =.

9.  Пространство l^m столбцов x=(x_k), состоящих из m чисел из R , с нормой ||x|| =.

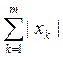10.  Пространство  столбцов x=(x_k), состоящих из m чисел из R , с нормой ||x|| =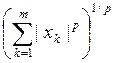

11.  Пространство l₁ последовательностей x=(x_k)_k³1 , состоящих из чисел из R , удовлетворяющих условию 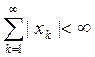, с нормой   ||x|| =.

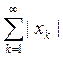12.  Пространство l₂ последовательностей x=(x_k)_k³1 , состоящих из чисел из R , удовлетворяющих условию  с нормой  ||x|| =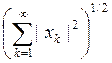

13.  Пространство l_p последовательностей x=(x_k)_k³1 , состоящих из чисел из R , удовлетворяющих условию 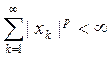,  с нормой  ||x|| =.

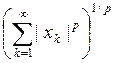14.  Пространство m ограниченных последовательностей x=(x_k)_k³1 , состоящих из чисел из R , с нормой  ||x|| = max { |x_k| : k ≥1}.

15.  Пространство c₀ сходящихся к 0  последовательностей x=(x_k)_k³1 , состоящих из чисел из R , с нормой  ||x|| = max { |x_k| : k ≥1}.

16.  Пространство c^m(a) столбцов x=(x_k), состоящих из m чисел из R , с нормой ||x|| =, где a= (a₁, a₂, …, a_m) – m-ка чисел a_i >0.

17.  Пространство l^m(a) столбцов x=(x_k), состоящих из m чисел из R , с нормой ||x|| =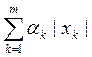 ,  где a =  (a₁, a₂, …, a_m) – m-ка чисел a_i >0.

18.  Пространство E^m(a) столбцов x=(x_k), состоящих из m чисел из R , с нормой ||x|| =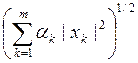,  где a =  (a₁, a₂, …, a_m) – m-ка чисел a_i >0.

19.  Пространство столбцов x=(x_k), состоящих из m чисел из R , с нормой ||x|| =.

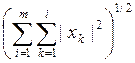20.  Пространство столбцов x=(x_k), состоящих из m чисел из R , с нормой ||x|| =max.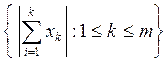

Дополнительные задачи.

1.  Разработать алгоритм приближения рациональными числами квадратного корня из рационального числа. (Что можно сказать о приближении алгебраических чисел рациональными?)

2.  Разработать алгоритм решения задачи Коши для уравнения Рикатти  , y(x₀)=y₀ .

3.  Множество C¹[a,b] всех непрерывно дифференцируемых на [a,b] функций с метрикой   является полным сепарабельным метрическим пространством.    (Сепарабельность вытекает из счетности множества многочленов с рац. коэф.)

4.  Доказать, что множество непустых замкнутых ограниченных подмножеств полного метрического пространства (M,d) с хаусдорфовой метрикой d_H полно.