Таблица 9.7
|
Матрица планирования |
220 |
280 |
200 |
100 |
|
||||
|
240 |
6,5 |
9,5 |
8,5 |
0 |
u1 = 0 |
||||
|
220 |
20 |
||||||||
|
360 |
6 |
6 |
7 |
0 |
u2 = –1,5 |
||||
|
280 |
80 |
||||||||
|
100 |
8 |
11 |
10 |
0 |
u3 = 0 |
||||
|
100 |
|||||||||
|
100 |
10 |
11 |
8 |
0 |
u4 = 0,5 |
||||
|
100 |
|||||||||
|
|
v1 = 6,5 |
v2 = 7,5 |
v3 = 8,5 |
v4 = 0 |
4640 |
||||
Из таблицы 9.7 оптимального плана получаем, что оптимальным вариантом прироста мощности является вариант строительства нового предприятия, так как вариант реконструкции приходится на «фиктивного» потребителя.
Полученное оптимальное решение является целочисленным, т.е. все мощности предприятий не дробятся между реальными и фиктивными потребителями.
Совокупность G двух множеств: А – множества вершин и С – множества дуг, называется графом. Т.е. G = (А, С).
![]() А – множество
объектов произвольной природы, С – множество формализованных связей
между ними.
А – множество
объектов произвольной природы, С – множество формализованных связей
между ними.
Геометрически вершины графа обозначаются: , а связи между ними – линиями, соединяющими вершины.
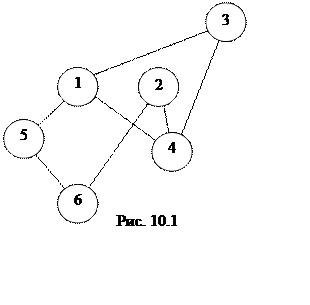 |
Довольно часто графы представляются в виде матрицы смежности вершин, в которой элементы с номерами i и j, соответствующие связанным вершинам, отмечаются единицей (1) или точкой (·), а соответствующие несвязанным вершинам – нулем (0)
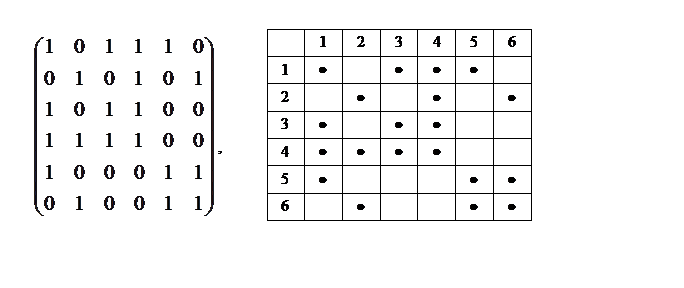 |
Часто в матрице смежности вершинам проставляются значения, которые характеризуют дуги. Например, если Cij – расстояние между вершинами, то матрица смежности превращается в матрицу расстояний. Если Cij – пропускная способность дуги, то C будет называться матрицей пропускных способностей. Если Cij – стоимость перевозки единицы груза из i в j, то С – матрица стоимостей.
Непрерывная последовательность связанных вершин называется цепью. Цепь, в которой начальные и конечные вершины совпадают, называется циклом.
Если любые две вершины графа можно соединить цепью, то он называется связанным, в противном случае – несвязанным. Связанный граф без циклов называется деревом-остовом или просто деревом.
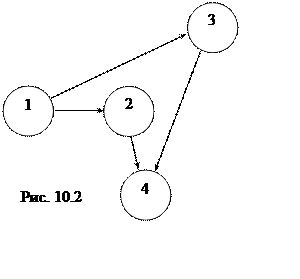
Если существует связь между вершиной i и вершиной j, но нет обратной связи, то соответствующая дуга, соединяющая эти вершины, называется ориентированной. Поэтому граф, в котором все дуги ориентированы, называется ориентированным. В нём геометрически дуги изображаются стрелками (рис. 10.2).
Транспортная задача (и ее варианты) – лишь одна из многочисленных задач, которые можно сформулировать и решить с помощью сетевых моделей.
Рассмотрим конкретные примеры:
 а) проектирование нефтепровода, соединяющего буровые скважины в
Каспийском море с находящейся на берегу приемной станцией. Следует выбрать
проект, в котором строительство нефтепровода имеет минимальную стоимость
(наименьшую протяженность);
а) проектирование нефтепровода, соединяющего буровые скважины в
Каспийском море с находящейся на берегу приемной станцией. Следует выбрать
проект, в котором строительство нефтепровода имеет минимальную стоимость
(наименьшую протяженность);
б) определение кратчайшего пути между двумя городами, проходящего по существующей сети шоссейных дорог;
в) определение максимальной пропускной способности (тонна/год) газопровода для транспортировки газа с мест добычи к месту переработки (потребления);
г) определение наиболее экономичной (имеющей минимальную стоимость) схемы транспортировки нефти из пунктов нефтедобычи на перерабатывающие заводы и далее в центры распределения (потребления). Здесь, помимо условий, определяющих верхний предел для добычи нефти и нижний предел для удовлетворения спроса на нее, необходимо принимать во внимание ограничения по мощности нефтеперерабатывающих (предприятий) заводов и пропускных способностей
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.