Экономико-математические методы: Учебно-практическое пособие по дисциплине «Математика». Часть 2

симметричного структурного преобразования условий прямой задачи в соответствии с правилами:

1)  каждому ограничению прямой задачи соответствует переменная двойственной задачи;

2)  каждой переменной прямой задачи соответствует ограничение двойственной задачи;

3)  коэффициенты при переменной (-й), фигурирующие в ограничениях прямой задачи, становятся коэффициентами левой части соответствующего ограничения двойственной задачи;

4)  коэффициент при переменной в целевой функции прямой задачи, становится постоянной правой части соответствующего ограничения двойственной задачи;

5)  постоянная правой части некоторого ограничения прямой задачи, становится соответствующим коэффициентом при переменной в целевой функции двойственной задачи;

6)  если прямая задача решается на максимум целевой функции, то двойственная задача решается на минимум, и наоборот. Переменные двойственной задачи не ограничены в знаке;

7)  если прямая задача решается на максимум, то ограничения в двойственной задаче имеют вид неравенства , если задача решается на минимум, то смысл неравенства противоположен.

Пример 7.1

Прямая задача:

,

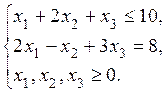
Стандартная форма прямой задачи:

,

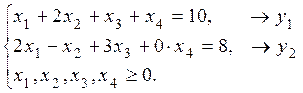
Двойственная задача:

                                

Из указанных правил следует: двойственная задача имеет  переменных (, , , ) и  ограничений (соответствующих  переменным прямой задачи , , , ).

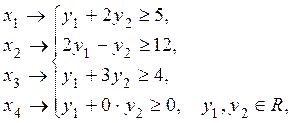
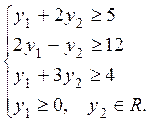
Доказано, что для каждой пары двойственных задач справедливы свойства:

1) для любой пары допустимых решений прямой и двойственной задач:

2) На любой итерации процесса решения прямой задачи:

3) для оптимальных решений прямой и двойственной задач значения целевых функций совпадают, т.е.

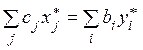,                                                      (7.1)

где звездочка (*)означает, что значения переменных берутся из оптимальных решений прямой и двойственной задач;

4) для каждой пары сопряженных условий в оптимальном решении выполняются следующие соотношения: если одно из них выполняется как простое равенство, то другое – как строгое неравенство и наоборот, т.е.

если 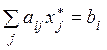, то ,                                              (7.2) 

если 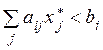,  то ,                                              (7.3)

если , то ,                                              (7.4)

если , то .                                              (7.5)

Опираясь на сформулированные свойства, можно дать следующую экономическую интерпретацию переменным двойственной задачи, которые в дальнейшем будем называть двойственными оценками.

1. Оценка ресурса показывает, на сколько изменится оптимальное значение целевой функции исходной задачи (суммарный объем выручки), если объем соответствующего ресурса изменить на единицу. Если же объем -го ресурса изменить на  единиц, то целевая функция изменится на величину  в случае, если это изменение не выйдет за границы устойчивости двойственных оценок.

2. Если ресурс в оптимальном плане израсходован полностью, то его оценка положительна (см. формулу (7.2)), если же ресурс не полностью израсходован в оптимальном плане, то его оценка равна нулю (см. формулу (7.3)). В первом случае ресурс является дефицитным, во втором – недефицитным. Для недефицитного ресурса значение соответствующей балансовой переменной покажет его остаток после выполнения оптимального плана. Чем больше оценка ресурса, тем он дефицитнее с точки зрения его вклада в поставленную цель – максимизировать суммарную выручку.

3. В оптимальный план включается производство только тех видов продукции, оценка ресурсов на производство единицы которых совпадает с ценой