Экономико-математические методы: Учебно-практическое пособие по дисциплине «Математика». Часть 1

словесно, качественно описываются взаимосвязи между элементами модели;

5.  вводятся символические обозначения для учитываемых характеристик экономического объекта и формализуются, насколько возможно, взаимосвязи между ними. Таким образом, формируется математическая модель объекта.

Следует различать математическую структуру модели и ее содержательную интерпретацию.

Пример 1.1

Пусть требуется определить, какую сумму следует положить в банк при заданной процентной ставке (20 % годовых), чтобы через год получить 12000 руб.?

Решение. Пусть начальный вклад составил . Конечная сумма (через год) известна  руб. Процент по вкладу составляет R = 20 % в год, т.е.

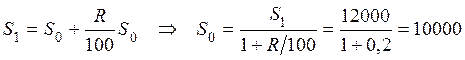 руб.

Пример 1.2

Пусть требуется определить, каков был объем выпускаемой продукции завода, если в результате технического перевооружения средняя производительность труда увеличилась на 20 %, и завод стал выпускать 12000 единиц продукции.

Решение. Пусть начальный объем выпуска продукции составлял  единиц, а конечный объем –  единиц. Процент прироста производительности труда обозначим через ;   R = 20 %. Обозначим через  – производительность труда. Предположим, что объем выпуска продукции прямо пропорционален производительности труда, т.е. , откуда получаем условие – 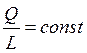, тогда

.

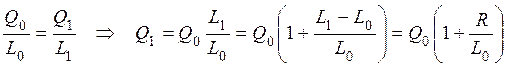Первоначальную производительность принимаем за 100 %, и получаем решение поставленной задачи:

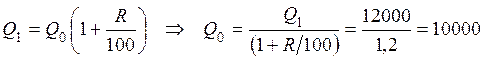 ед.

Математическая форма (структура) модели:

, и числовые значения входящих в нее величин одинаковы, однако экономическая ситуация, описываемая моделью, т.е. экономическая интерпретация модели и результатов расчета различны.

Таким образом, одни и те же модели и методы могут быть использованы для решения разных экономических задач.

Математическая модель экономического объекта – это его однозначное отображение (представление) в виде совокупности уравнений, неравенств, логических отношений, графиков, функциональных зависимостей.

Однозначное отображение объединяет группы отношений между элементами изучаемого объекта в аналогичные отношения между элементами модели. Иными словами, математическая модель – это условный образ объекта, построенный для упрощения его исследования.

Изучение модели дает новые знания об объекте, либо позволяет определить наилучшее решение в той или иной ситуации.

Основные элементы математической модели (рис. 1.1)

Экзогенные переменные – это те переменные, которые задаются вне модели, т.е. известны заранее.

Эндогенные переменные – это те переменные, которые определяются в ходе расчетов по модели и не задаются в ней извне.

Параметры– это коэффициенты уравнений (неравенств), функциональных зависимостей модели.

Часто экзогенные переменные и параметры в модели не разделяют.

Рассмотрим конкретную ситуацию.

Пусть имеется фирма, выпускающая несколько видов продукции. В процессе производства используются три вида ресурсов: оборудование, рабочая сила и сырье. Эти ресурсы однородны, количества их известны и в данном производственном цикле неизменны.

Задан расход каждого ресурса на производство единицы продукции каждого вида. Заданы цены на произведенную продукцию. Нужно определить объем производства с целью получения максимальной стоимости произведенной продукции (или в предположении, что вся она будет реализована, найдет сбыт на рынке) – общей выручки от реализации.

Решение. Каждый вид продукции должен иметь свой индекс, пусть  – индекс продукта,  (n число видов продукции).

В рассматриваемой задаче экзогенные переменные: имеющееся количество оборудования ; имеющееся количество рабочей силы ; имеющийся