Министерство образования и науки РФ
ГОУВПО «Комсомольский-на-Амуре государственный технический университет»
Кафедра МОП ЭВМ
по математической логике и теории алгоритмов
Выполнил: Рогозин В.А.
Группа: 4ВС-1
Вариант 19
Проверил: Хусаинов А.А.
Комсомольск-на-Амуре
2005
Для
произвольного целого числа ![]() , через
, через ![]() обозначим значение, равное 0 при чётных
обозначим значение, равное 0 при чётных ![]() , и равна 1 – при нечетных
, и равна 1 – при нечетных ![]() . Булевы функции
. Булевы функции ![]() и
и
![]() заданы с помощью операций сложения и
умножения целых чисел и функций
заданы с помощью операций сложения и
умножения целых чисел и функций ![]() . Равны ли эти функции?
Какие переменные из этих функций являются несущественными?
. Равны ли эти функции?
Какие переменные из этих функций являются несущественными?
![]()
![]()
![]()
![]()
|
|
|
|
f |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
|
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
0 |
|
1 |
1 |
1 |
1 |
|
|
|
g |
|
0 |
0 |
0 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
Не существенной является переменная х1
|
|
|
f |
|
0 |
0 |
0 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
Требуется составить таблицу истинности булевой функции, заданной с помощью логических связок и функции отрицания:
![]()
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
1 |
0 |
1 |
1 |
|
0 |
0 |
1 |
1 |
1 |
0 |
0 |
|
0 |
1 |
0 |
0 |
0 |
1 |
1 |
|
0 |
1 |
1 |
0 |
1 |
0 |
1 |
|
1 |
0 |
0 |
0 |
1 |
0 |
1 |
|
1 |
0 |
1 |
0 |
1 |
0 |
1 |
|
1 |
1 |
0 |
0 |
1 |
0 |
1 |
|
1 |
1 |
1 |
0 |
1 |
0 |
1 |
Привести к
совершенно дизъюнктивной нормальной форме заданную булеву функцию ![]() . Знак логического умножения ‘&’
опускается.
. Знак логического умножения ‘&’
опускается.
![]()
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
|
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
|
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
|
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
|
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
|
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
|
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
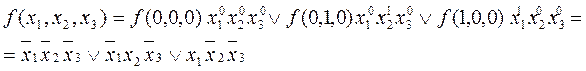
Булева функция ![]() задана с помощью таблицы. Найти её минимальную
дизъюнктивную нормальную форму методом карт Карно.
задана с помощью таблицы. Найти её минимальную
дизъюнктивную нормальную форму методом карт Карно.
|
|
00 |
01 |
11 |
10 |
|
00 |
1 |
1 |
0 |
0 |
|
01 |
0 |
0 |
1 |
1 |
|
11 |
0 |
0 |
1 |
1 |
|
10 |
1 |
1 |
0 |
0 |
Решение. Противоположные точки на границах области
определения ![]() можно считать находящимися рядом. Поэтому
разобьем область, на которой
можно считать находящимися рядом. Поэтому
разобьем область, на которой ![]() на два квадрат
на два квадрат ![]() , 1-й: объединим точки
, 1-й: объединим точки ![]() ,
, ![]() ,
, ![]() ,
, ![]() , 2-й
, 2-й ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Этим
квадратам соответствует логическое произведение
. Этим
квадратам соответствует логическое произведение ![]() и
и ![]() . Значит,
. Значит, ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.