Решение систем нелинейных уравнений. Форматы функций.

Лабораторная работа 5

Часть I

Решение систем нелинейных уравнений

Цель работы:

-  изучить форматы некоторых встроенных функций;

-  освоить приемы решения систем нелинейных уравнений;

-  приобрести навыки решения простейших инженерных задач.

.

Задание 1. Ответить на следующие контрольные вопросы из лекции 5:

- как отыскать корни нелинейных уравнений в системе MathCAD;

- как решить систему нелинейных уравнений в MathCAD’e;

- что должен делать пользователь, если MathCAD не может найти  корни;

- как графически проверить наличие действительных корней системы двух уравнений;

- как задать точность поиска корней;

- как найти корни при аналитических преобразованиях;

- перечислите способы решения системы линейных уравнений в системе        MathCAD;

- как решить обыкновенное дифференциальное уравнение в системе MathCAD;

- выполнить пример 5.1 в системе MathCAD;

- как решить систему двух дифференциальных уравнений.

Задание 2. Решить два нелинейных уравнения с точностью до 0.0001:

a∙x³+ b∙x² + c∙x +d = 0 и f₁(x) + f₂(x) = f₃(x)

Вместо компонентов a, b, c, d, f₁(x), f₂(x) и f₃(x) записать значения из табл. 5.1.   Корни отделить графически.

Таблица 5.1

Варианты компонентов функций

номер вар.	1) Коэффициенты полинома:				2) Тригонометрическое уравнение:
	а	b	c	d	f1(x)	f2(x)	f3(x).
1	1	-3	0	2	sin(x)	cos(2x)	-1
2	2	-5	0	1	sin(2x)	cos(x)	0.7
3	3	-7	2	2	sin(1.5x)	cos(x)	sin(x/3)
4	2	-6	1	2	sin(1.5x)	cos(x)	cos(x/3)
№	а	b	c	d	f1(x)	f2(x)	f3(x).
5	-3	-4	1.5	1	√(1.5x)	-cos(x)	x/3+0.5
6	-1.5	5	4	-10	acos(x/4)	cos(2x)	sin(x)
7	-4	10	0	-6	acos(x/4)	cos(x)	sin(2x)+2
8	-4	0	6	-1	asin(x/4)	cos(x)	sin(2x)
9	-1	-1	5	0	asin(x/5)	sin(x)	cos(2x)
10	-2	-3	2	2	asin(x/5)	sin(2x)+1	cos(x)
11	-0.5	-3	5	1	ex	sin(2x)	cos(x/3)
12	1	-1	-1	0	ex	-sin(2x)	-sin(x/3)
13	2	-3	-3	3	e-x	sin(2x)	sin(x/3)-0.75
14	2.5	-4	-2	2	e-x	cos(x)	sin(x/2)+0.6
15	10	-10	-5	2	cos(x)+3	e-x	ln(5x)
16	5	-5	-3	1	sec(x/8)	-e-x	sin(2x)+1
17	4	-4	-6	1	sec(x/8)	e-x-2	cos(2x)
18	3	-3	-8	5	sec(x/7)-2	e-x	cos(2x)
19	-2	-7	-0.2	6	sec(x/7)-2	e-x	sin(x)
20	-3	-7	-0.5	3	sec(x/6)	e-x-2	sin(3x)
21	-2	-6	2	10	atan(x/5)	e-x-1	sin(x)
22	-1	-2	2	2	atan(x/4)	e-x-1	cos(x)
23	2	3	-5	-5	atan(x/3)	ex	cos(x)
24	2	1	-8	-2	atan(x/2)	sin(x)	cos(x)
25	1	2	-6	-3	atan(x/2)	sin(2x)	cos(x)
26	3	1	-5	-1	(x+10)-1	sin(x)+0.5x	cos(x)-1
27	3	3	-4	-3	(x+10)-1	0.5x	cos(2x)+1
28	4	4	-4	-2	(x+10)-1	-0.5x	cos(x)-0.7
29	7	-5	-10	3	(x+10)-1	-0.5x	sin(x)-1.5
30	8	-4	-7	0	(x+10)-2	-0.4x	sin(x)-1.5

     Задание 3. Решить систему двух нелинейных уравнений с точностью до 0.0001:

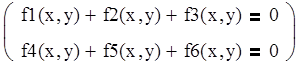Вместо компонентов f1(x), f2(x), f3(x), f4(x), f5(x) и f6(x) записать значения из табл. 5.2.  Корни отделить графически.

Таблица 5.2

Варианты компонентов функций системы уравнений

номер вар.	Компоненты 1-го уравнения			Компоненты 2-го уравнения
	f1(x,y)	f2(x,y)	f3(x,y)	f4(x,y)	f5(x,y)	f6(x,y)
1	sin(x+1)	2	-y	x	cos(y)	-1
2	cos(x+1)	3	-y	1	sin(y)	x
3	cos(x+1)	x	-y	x	2	5 sin(y)
4	-y	2x	sin(x+0.5)	-x	-3sin(y)	-1
5	2	-y	5sin(x+0.5)	10-y	-x	7sin(y)
6	0	5sin(x/3)	-y	-x	4sin(y/3)	10-2y
7	-y	6cos(x/3)	3	5-1.5y	-x	-3sin(y/3)
8	6cos(x/3)	3	-y	-x	-atan(y/5)	5
9	1	5sin(x/2)	-y	-atan(y/2)	-x	5sin(y/4)
10	-y	3	6cos(x)	-x	4cos(y/4)	-atan(y/2)
№	f1(x,y)	f2(x,y)	f3(x,y)	f4(x,y)	f5(x,y)	f6(x,y)
11	-y	6cos(x)	3	-x	-asec(y+6)	8cos(y/4)
12	6sin(x)	3	-y	-asec(y+5)	-x	6sin(y/4)
13	5sin(x)	-y	2	-x	-asec(y-8)	4sin(y/3)
14	-y	8acot(2x)	x	-x	4sin(y/3)	-asec(y-8)
15	-y	5acot(x/2)	3x	-x	-asec(y-6)	4cos(y/2)
16	5cos(x)	-y	2sin(x)	-y+6	-x	10sin(y/3)
17	sin(x)	5cos(x/2)	-y	-x	-y/3	6sin(y/4)
18	-y	-cos(x)	2cos(x/3)	y/2	-x	4cos(y)
19	-y	-5cos(x/2)	x/2	-x	y/2	4cos(y)
20	-y	-5sin(x/2)	-x/2	-x	y/2	4cos(-y)
21	-y	-x	-5sin(x/2)	-x	10cos(-y)	y/3
22	-y	-5cos(-x/2)	-x	-x	y/3	10sin(y)
23	x	-y	5cos(x/2)	-x	-y/3	-10sin(2y)
24	-y	0	(5-x)/(10+x)	-x	-y/2	-10sin(y)
25	-y	0	(x-5)/(x-10)	-x	-(y-5)/(y+10)	-10sin(y)
26	-y	cos(x/5)	5sin(x+1)	-x	3cos(y+1)	sin(x/4)
27	-y	cos(x/5)	5cos(x+1)	-x	3sin(y+1)	sin(x/4)
28	-y	cos(2x)	5sin(x/2)	-x	3sin(y)	cos()y/3
29	-y	cos(x/2)	10sin(x)	-x	2sin(y)	3cos(y/3)
30	-y	-cos(x/3)	10sin(x)	-x	-2sin(y)	3cos(y/4)

Задание 4. Решить дифференциальные  уравнения первого и второго порядка с точностью до 0.0001:

с помощью функций Odesolve() и rkfixed(). Вместо компонентов f(t,y(t)), a,b,c, f(x) записать значения из табл. 5.3. Результаты, полученные разными функциями сравнить. Отсутствующие начальные условия выбрать самостоятельно.

Таблица 5.3

Варианты компонентов функций дифференциальных уравнений

номер вар.	Компоненты дифф/ур-ия 1-го порядка			Компоненты дифф/ур-ия 2-го порядка
	f(t,y)	t0	y0	a	b	c	d	f(x)
1	e-y+10t	0	1	20	30	0	0	100sin(x)
2	y-2-sin(t)2	0	2	50	30	10	0	100sin(x)
3	√y – sin(t)	0	3	50	60	20	0	100sin(x/2)
4	√y + cos(t)	0	4	20	30	0	0	100sin(x/2)
5	cos(t) -y	0	5	80	30	10	0	50sin(x/3)
6	cos(t/2) - y	0	1	80	100	10	0	50sin(x/3)
7	t2 - y	0	2	80	100	50	-25	50sin(x/4)
8	-y∙ t	0	3	20	30	0	0	100cos(x)
9	-y2∙ t	0	4	50	30	10	0	100cos(x)
10	(-y)2	0	5	50	60	20	0	100cos(x/2)
11	√y - cos(t)	0	1	20	30	0	0	100cos(x/2)
12	y∙sin(2t)	0	2	80	30	10	0	50cos(x/3)
№	f(t,y)	t0	y0	a	b	c	d	f(x)
13	y/4∙cos(2t)	0	3	80	100	10	0	50cos(x/3)
14	√(y +t)	0	4	80	100	50	-25	50cos(x/4)
15	√(sin(y) +t2)	0	5	80	100	50	-25	x-125sin(x)
16	√t+5cos(y)	0	1	40	10	50	-25	x-125sin(x/3)
17	t+25cos(t)	0	2	40	0	50	-50	x-125sin(x/3)
18	t-25cos(t)	0	3	100	0	10	-50	x-200sin(x/3)
19	t+25sin(t)	0	4	10	20	0	-50	x-300sin(x/2)
20	t-25sin(t)	0	5	80	100	50	-25	x-125cos(x)
21	y∙sin(y)	0	1	40	10	50	-25	x-125cos(x/3)
22	y∙sin(t)	0	2	40	0	50	-50	x-125cos(x/3)
23	y∙cos(t)	0	3	100	0	10	-50	x-200cos(x/3)
24	-y∙cos(t)	0	4	10	20	0	-50	x-300cos(x/2)
25	-y∙sin(t)	0	5	100	200	5	50	10-300sin(x)
26	-t∙tan(y)	0	1	200	100	50	50	10-300sin(x)
27	-y∙tan(y)	0	2	200	300	0	50	10-300sin(x)
28	-y2∙tan(y)	0	3	100	200	5	50	10-300cos(x)
29	-y∙tan(y)2	0	4	200	100	50	50	10-300cos(x)
30	-y∙cot(y)2	0	5	200	300	0	50	10-300cos(x)

Задание 5. Решить систему двух дифференциальных  уравнений первого порядка с точностью до 0.0001:

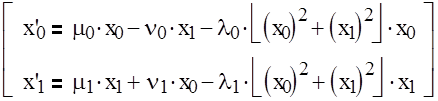Вместо компонентов μ₀, ν₀, λ₀, μ₁, ν₁, λ₁, x₀, x₁ записать значения из табл. 5.4.

Таблица 5.4

Варианты компонентов функций системы уравнений

номер вар.	Компоненты 1-го дифф/ур-ия			Компоненты 2-го дифф/ур-ия			Начальн_усл
	μ0	ν0	λ0	μ1	ν1	λ1	x0	x1
1	-0.2	1	1	-0.2	1	1	0	1
2	-0.2	1	1	-0.1	0.5	0	0	3
3	-0.2	1	0	-0.4	0.5	1	3	0
4	-1	1	1	-0.4	-1.5	0	3	0
5	-1	0	1	-0.4	-1.5	2	2	0
6	-0.5	-1	1	-0.4	-1.5	1	0	1
7	-1	-1	-1	-1	-2.5	-1	1	3
8	-0.4	1	1	-0.1	1	0.5	0	1
9	-0.1	1	1	-0.4	-1	0	0	2
10	-0.1	1	1	-0.1	-1	1	0	1
11	0	1	1	-0.1	-1	0	0	2
12	0	1	0	-0.1	1	1	1	2
13	0.1	1	2	0	0.5	1	1	0
№	μ0	ν0	λ0	μ1	ν1	λ1	x0	x1
14	0.1	0.5	2	0.1	0.5	2	2	0
15	0.1	0.75	2	0.2	0.75	1	0	2
16	0.2	0.75	1	-0.2	0.75	2	1	2
17	1.2	0.5	2	-1.2	-1	1	1	0
18	1	0.5	2	-1	-0.5	1	1	1
19	1	0.5	1	1	0.5	1	1	-1
20	1	1	1	1	1	0.5	-1	-1
21	0	2	0.5	1	1	0.5	-1	-1
22	0.05	2	0.5	-0.05	2	0.5	-1	0
23	0.15	0	0.5	-0.15	2	0	-1	0
24	-0.15	0.75	1.5	-0.15	0.75	1.5	-1	0
25	-0.15	0.75	1	-0.25	1	1.5	1	0
26	-0.25	0.75	0.75	-0.25	1.5	1.5	1	1
27	-0.25	0.5	0.75	-0.5	2.5	1.5	0	1
28	-0.2	0.75	1.75	-0.25	1.5	1.5	1	1.5
29	3	1.75	0.75	-0.35	1.5	0.5	0	1.5
30	0.3	0.75	0.75	-0.35	1.5	1.5	0	2

Лабораторная работа 5

Часть II

Использование функций интерполирования, регрессии

 и предсказания

Цель работы:

-  изучить форматы функций интерполирования, регрессии, предсказания;

-  освоить приемы выполнения интерполирования, регрессии, предсказания;

-  приобрести навыки решения простейших инженерных задач.

Задание 1. Ответить на следующие контрольные вопросы из лекции 5:

- методика выполнения линейной интерполяции в системе MathCAD;

- методика выполнения интерполяции кубическим сплайном;

- сущность линейного предсказания и ее реализация;

- сущность линейной регрессии и ее реализация;

- сущность полиномиальной регрессии и ее реализация.

Задание 2. Задать табличную функцию для интерполяции следующим образом:

-  для х использовать дискретный аргумент i := 0..10  x_i := i

-  для функции y использовать датчик случайных чисел y_i := rnd(10).

Вычислить значения функции y для любых двух промежуточных аргументов x₁ и x_2,  используя встроенную  функцию линейной интерполяции. Выполнить проверку результатов вычисления с помощью программы расчета точек прямой, проходящей через две заданные точки плоскости. Выполнить интерполяцию с помощью кубического сплайна и построить совмещенные диаграммы табличной функции, линейной и кубической интерполяции.

Задание 3. Выполнить аппроксимацию табличной функции (см. задание 2) из условия минимизации ошибки. В отличие от функций интерполяции, аппроксимирующая кривая должна проводиться из условия минимума среднеквадратичного отклонения. Использовать  следующие функции:

- линейную функцию (описывается уравнением y=k×x+b. Значения k и b найти с помощью встроенных функций slope(vx,vy) и intercept(vx, vy);

-  полином n-й степени (использовать функции regress(vx, vy, n), interp(), loess(vx,vy,span)).

Построить совмещенные графики табличной функции, линейной и полиномиальной регрессии. Для оценки погрешности вычислить среднеквадратическое отклонение по формулам:

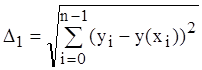 -для линейной регреcсии;

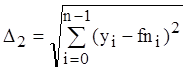 - для полиномиальной регреcсии;

-  с помощью набора полиномов (используются функции vn: = loess(vx, vy, m),     fc_i = interp(vn, vx, vy, vx_i)). Для оценки погрешности вычислить среднеквадратическое отклонение по формуле:

.

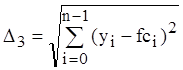Задание 4. Оценить табличную функцию (см. задание 2) за пределами ее области данных (использовать функцию predict(v,m,n). Построить совмещенные графики табличной функции и функции предсказания.

Лабораторная работа 6

Программирование в MathCAD’e

Цель работы:

Научиться разрабатывать и использовать простейшие цикловые программы на алгоритмическом языке MathCAD.

Задание 1.Ответить на следующие контрольные вопросы из лекции 6:

- как вызвать панель программирования;

- изложить правила заполнения полей шаблонов программирования;

- выполнить пример 4.2 с использованием простейшей программы линейной структуры, представленной на рис. 6.3;

- какие операторы используются в программах с разветвляющейся структурой;

- выполнить примеры 6.1 и 6.2;

- какие операторы используются в программах с цикловой структурой;

- изложить методику отыскания изолированных действительных корней функции f(x)=0;

- выполнить пример 6.3 и провести анализ входных и выходных параметров программы otd(); изложить алгоритм отделения корней;

- выполнить примеры 6.4 и 6.5 и провести анализ входных и выходных параметров программ pol() и xord(); изложить алгоритмы метода половинного деления и метода хорд; сравнить быстродействие методов;

- указать назначение операторов управления и дать их краткую характеристику и правила заполнения полей их шаблонов;

- выполнить пример 6.6 и проанализировать два режима работы программы;

- изложить сущность алгоритма отыскания корней методом Ньютона