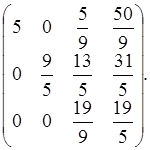
На третьем шаге зануляем элементы а13 и а23 с помощью третьего уравнения. Для этого умножим третье уравнение на -117/95 и прибавим ко второму, умножим третье уравнение на -5/19 и прибавим к первому, получим:
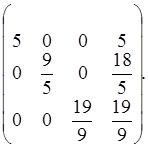
Мы получили систему линейных уравнений с диагональной матрицей. На этом прямой ход метода Гаусса – Жордана закончен.
Обратная подстановка
В данном случае обратная подстановка заключается в решении системы линейных уравнений с диагональной матрицей:
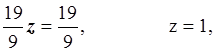
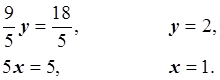
Ответ: x = 1, y = 2, z = 1.
Задача 4
Построить и обосновать алгоритм решения системы линейных уравнений методом итераций с точностью ε:
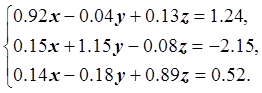
Оценить число шагов k, необходимых для достижения точности ε.
Решение
1. Необходимо обосновать, что определитель матрицы не равен нулю:
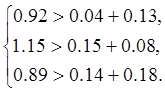
Следовательно, матрица А является матрицей с диагональным преобладанием, значит, det A ≠ 0.
2. В нашем случае
можно считать: ![]() , где
, где ![]() –
единичная матрица, тогда D
= b.
–
единичная матрица, тогда D
= b.
Найдем С и докажем, что ![]() :
:
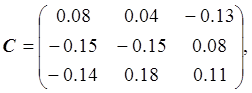
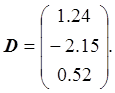
Вычислим первую норму С:
![]() .
.
Следовательно, метод итераций сходится для любого x0, выбираем вектор начального
приближения: ![]() .
.
3. Формула метода: ![]() .
.
4. Условие остановки итерационного процесса:
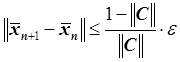 ,
, ![]() .
.
5. Оценка числа шагов k, необходимых для достижения точности ε:
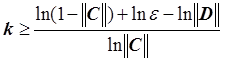 ,
, ![]() ,
, ![]() .
.
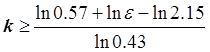 .
.
При выполнении этого условия х(k) является приближенным решением системы линейных уравнений с точностью e, полученным методом итераций.
3. Численные методы решения систем линейных уравнений....................................................................................... 25
3.1. Метод Крамера.......................................................................................................................................................................................................... 27
3.2. Метод Гаусса............................................................................................................................................................................................................. 27
3.3. Метод Гаусса с частичным выбором ведущего элемента............................................................................................................................ 30
3.4. Вычисление определителя матрицы.................................................................................................................................................................... 32
3.5. Нахождение обратной матрицы........................................................................................................................................................................... 33
3.6. Метод Гаусса-Жордана.......................................................................................................................................................................................... 33
3.7. Итерационные методы решения системы линейных уравнений................................................................................................................. 34
3.8. Метод итераций......................................................................................................................................................................................................... 34
3.9. Метод Зейделя............................................................................................................................................................................................................ 38
3.10. Число обусловленности матрицы...................................................................................................................................................................... 39
3.11. Корректность задачи решения систем линейных уравнений.................................................................................................................... 42
3.12. Примеры решения задач....................................................................................................................................................................................... 42
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.