Численные методы решения систем линейных уравнений, страница 7

       

           

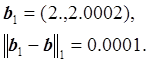
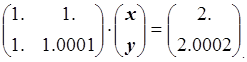
Решение этой системы уравнений:

,                 .

.

Вектор b изменился незначительно, а вектор x изменился значительно. С чем это связано? Это связано со свойствами матрицы А.

Определение. Матрица А системы линейных уравнений  называется плохо обусловленной, если малые изменения в векторе b  приводят к большим отклонениям в решении x, т.е.:

,             ,

,       но .

Решение системы линейных уравнений с плохо обусловленной матрицей – это решение некорректно поставленной задачи.

Отметим, что плохая обусловленность – это свойство матрицы и, естественно, оно сказывается при численном решении систем линейных уравнений. Точное решение является неустойчивым, следовательно, и численное решение будет неустойчивым. Для численного решения таких задач используются специальные методы, учитывающие некорректность задачи.

Существует характеристика матрицы А, называемая числом обусловленности, которая указывает, является матрица плохо обусловленной или нет.

То есть  для каждой матрицы до решения системы линейных уравнений мы можем вычислить число, называемое числом обусловленности и обозначаемым cond(A) и определить, хорошо обусловлена матрица или нет. Если cond(A) > 1000, то матрица считается плохо обусловленной.

Как найти cond(A)? Для его вычисления используются значения собственных чисел матрицы А.

Напомним определение собственного числа и собственного вектора матрицы А.

Определение. Число l называется собственным числом квадратной матрицы А, если существует ненулевой вектор x, такой что

.

Напомним некоторые свойства собственных чисел матрицы.

У симметричной  матрицы все собственные числа вещественные,   тогда и только тогда, когда , у симметричной, положительно определенной матрицы все собственные числа больше нуля.

Матрица называется положительно определенной, если для любого ненулевого вектора  справедливо:  , где () – скалярное произведение векторов a и b.

Определение. Если А – симметричная положительно определенная матрица, то число обусловленности равно:

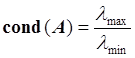 , где   – максимальное собственное число матрицы А;           – минимальное собственное число матрицы А.

Обсудим это определение. Так как А – симметричная и положительно определенная матрица, то , следовательно, , следовательно,

    и   

Дадим определение для произвольной квадратной матрицы А.

Определение. Для произвольной квадратной матрицы А число обусловленности равно:

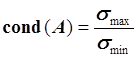, где  – сингулярные числа матрицы А.

Сингулярные числа  матрицы А определяются следующим образом:

, где    – собственные числа матрицы  .

Обсудим это определение.  – симметричная неотрицательно определенная матрица.

, следовательно,   все  – вещественные числа, .

,                .

Если А – вырожденная матрица, то  (так как ). Число обусловленности характеризует близость А в вырожденной матрице. Чем больше  тем ближе А по своим свойствам к вырожденной матрице.

Отметим свойство числа обусловленности:

.

Утверждение. Число обусловленности матрицы выполняет роль множителя в увеличении относительной ошибки. Изменения в правой части системы линейных уравнений могут повлечь за собой изменения в решении не больше, чем  раз:

,

 .

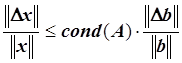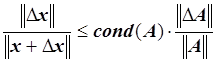Пример 2

Пусть А – матрица системы линейных уравнений . При  вектор . Найти решение  системы линейных уравнений  при  и объяснить полученный результат.

Решение

Матрицу А, вектора  возьмем из предыдущего примера:

,         ,             ,

,                .

,            .

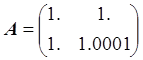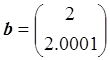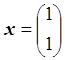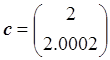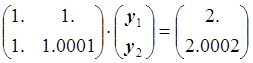Малые изменения в векторе правой части привели к большим изменениям в решении:

          

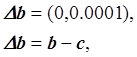
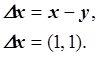
,             .0001  ,           ,        ,

,        .

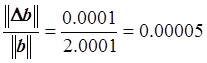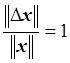Почему это произошло? Вычислим число обусловленности матрицы А:

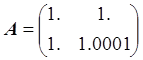,         А – симметричная матрица.

Необходимо определить, является ли А положительно определенной. Это можно доказать, используя определение положительной определенности, а можно воспользоваться следующим утверждением.

Утверждение. Если все главные миноры матрицы А больше нуля, то матрица А  положительно определенная.