В нашем случае M1
= 1 и M2 = ![]() (M1,
M2 – главные миноры
матрицы А), следовательно, А –
положительно определенная матрица, поэтому можно использовать формулу:
(M1,
M2 – главные миноры
матрицы А), следовательно, А –
положительно определенная матрица, поэтому можно использовать формулу:
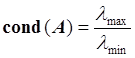 .
.
Найдем собственные числа матрицы А.
Воспользуемся следующим утверждением:
Утверждение. Число ![]() является собственным числом матрицы А с
соответствующим ненулевым собственным вектором тогда и только тогда, когда
является собственным числом матрицы А с
соответствующим ненулевым собственным вектором тогда и только тогда, когда
![]() .
.
Запишем уравнение:
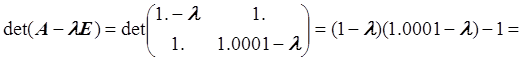
![]() .
.
![]() ,
,
![]() .
.
![]() ,
, ![]() .
.
![]() , следовательно, матрица А – плохо обусловленная.
, следовательно, матрица А – плохо обусловленная.
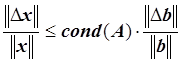 .
.
Для корректности задачи решения системы линейных уравнений требуется одновременное выполнение двух условий:
1. Матрица А системы линейных уравнений является невырожденной.
2. Матрица А является хорошо
обусловленной, ![]() .
.
Если нарушается первое условие, то система линейных
уравнений ![]() либо не имеет решения, либо имеет
бесконечное множество решений. Если нарушается второе условие, то решение
системы линейных уравнений
либо не имеет решения, либо имеет
бесконечное множество решений. Если нарушается второе условие, то решение
системы линейных уравнений ![]() является неустойчивым,
то есть малые изменения b могут
привести к большим изменениям x.
является неустойчивым,
то есть малые изменения b могут
привести к большим изменениям x.
Таким образом, если не выполняется хотя бы одно из этих
условий, то задача решения системы линейных уравнений не является корректно
поставленной. Если нарушается условие два, то для численного решения системы
линейных уравнений необходимо использовать специальные методы решения систем
линейных уравнений, ориентированные на плохо обусловленные матрицы (например,
регуляризацию по Тихонову). Отметим, что значение определителя матрицы А не является характеристикой обусловленности матрицы. Такой
характеристикой является число обусловленности матрицы А ![]() .
.
Пример
Рассмотрим диагональную матрицу размерностью 100, на
главной диагонали стоят числа 0.1. Определитель такой матрицы равен ![]() , а число обусловленности такой матрицы
равно: 1 (
, а число обусловленности такой матрицы
равно: 1 (![]() ), и решение такой системы линейных
уравнений является корректно поставленной задачей.
), и решение такой системы линейных
уравнений является корректно поставленной задачей.
Задача 1
Построить LU-разложение матрицы А. Вычислить значение определителя матрицы А методом Гаусса:
А=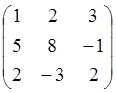 .
.
Решение
Умножим первую строку на -5 и прибавим ко второй. Умножим первую строку на –2 и прибавим к третьей. Получим:
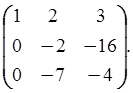
Умножим вторую строку на –7/2 и прибавим к третьей. Получим матрицу:
U = 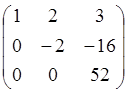 и матрицу
L =
и матрицу
L = 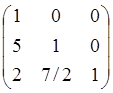 .
.
Определитель матрицы А находим по
формуле: 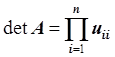 , det A = -104.
, det A = -104.
Задача 2
Решить систему линейных уравнений методом Гаусса с частичным выбором ведущего элемента (по столбцу):
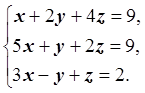
Решение
Прямой ход метода Гаусса
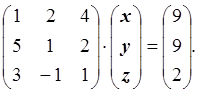
Прежде всего, выбираем максимальный по модулю элемент в первом непреобразованном столбце:
![]() ,
, ![]() , следовательно, ведущим элементом
является 5.
, следовательно, ведущим элементом
является 5.
Ведущим элементом является элемент ![]() ,
поэтому необходима перестановка строк 1 и 2:
,
поэтому необходима перестановка строк 1 и 2:
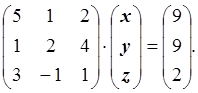
Умножим первое уравнение на –1/5 и прибавим ко второму. Умножим первое уравнение на –3/5 и прибавим к третьему. Получим:
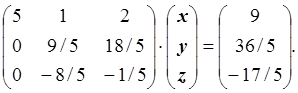
Рассмотрим следующий непреобразованный столбец:
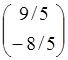 ,
, 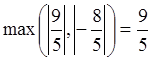 , следовательно, ведущим элементом
является 9/5, перестановка строк не требуется. Умножим второе уравнение на 8/9
и прибавим к третьему. Получим:
, следовательно, ведущим элементом
является 9/5, перестановка строк не требуется. Умножим второе уравнение на 8/9
и прибавим к третьему. Получим:
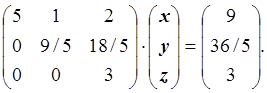
Мы получили систему линейных уравнений с верхней треугольной матрицей. Прямой ход метода Гаусса с частичным выбором ведущего элемента закончен.
Обратная подстановка
3z = 3, z = 1,
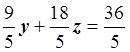 , y = 2,
, y = 2,
5x + y + 2z = 9, x = 1.
Задача 3
Решить систему линейных уравнений методом Гаусса-Жордана с частичным выбором ведущего элемента:
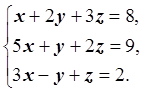
Решение
Прямой ход
В методе Гаусса-Жордана первый шаг прямого ходя совпадает с первым шагом прямого хода метода Гаусса. Найдём максимальный по модулю элемент первого столбца (это элемент а21), поменяем местами первое и второе уравнения, получим:
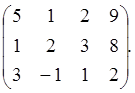
Умножим первое уравнение на –1/5 и прибавим ко второму, умножим первое уравнение на –3/5 и прибавим к третьему, получим:
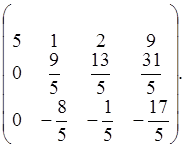
На втором шаге непреобразованный столбец состоит из двух элементов: 9/5, -8/5. Максимальный по модулю элемент расположен на главной диагонали, следовательно, не нужно менять местами уравнения. Чтобы занулить элементы а32 и а12 , умножим второе уравнение на 8/9 и прибавляем к третьему, умножаем второе уравнение на –5/9 и прибавим к первому, получим:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.