Численные методы решения систем линейных уравнений, страница 4

Рассмотрим метод Гаусса с частичным выбором ведущего элемента с точки зрения операций над матрицами.

Теорема

Произвольная невырожденная матрица перестановкой строк (столбцов) может быть приведена к матрице с главными минорами, отличными от нуля (, где P – матрица перестановок).

Матрица Р получается из единичной матрицы перестановкой строк (столбцов).

Сложность метода Гаусса с частичным выбором ведущего элемента

Число арифметических действий, необходимых для его реализации: , где n – число уравнений. Оценим сложность по памяти: требуется память для хранения n² элементов матрицы, вектора b (n элементов) и вектора x (n элементов), в результате, .

Метод Гаусса с частичным выбором ведущего элемента является устойчивым, если все ведущие элементы по модулю больше единицы.

Следует отметить, что метод Гаусса с частичным выбором ведущего элемента – это основной алгоритм вычислительной математики линейной алгебры.

Метод Гаусса с полным выбором ведущего элемента отличается от метода Гаусса с частичным выбором ведущего элемента тем, что на каждом шаге прямого хода ведущий элемент ищется в непреобразованной части матрицы. Непреобразованная часть матрицы – это квадратная матрица размерности n-i+1, получаемая вычеркиванием первых   i – 1  строк и первых   i – 1  столбцов. В методе Гаусса с полным выбором ведущего элемента возможна не только перестановка строк матрицы и соответствующих элементов правой части, но и перестановка столбцов матрицы и, соответственно, изменение порядка следования неизвестных.

3.4. Вычисление определителя матрицы

Мы знаем, что в методе Гаусса с частичным выбором ведущего элемента , где P – матрица перестановок, т.е. матрица, полученная из единичной матрицы перестановкой строк, следовательно, , где  – число перестановок строк.

Получим:                        .

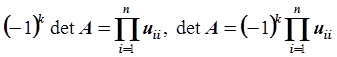Окончательная формула для вычисления определителя матрицы А:

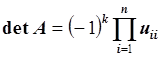, где  – число перестановок строк в методе Гаусса с частичным выбором ведущего элемента;  – ведущие элементы матрицы, полученные методом Гаусса с частичным выбором ведущего элемента.

Таким образом, при решении системы линейных уравнений методом Гаусса с частичным выбором ведущего элемента мы одновременно с решением получаем значение определителя матрицы. Если же при использовании метода Гаусса с частичным выбором ведущего элемента мы получаем, что ведущий элемент равен нулю, то detA = 0.

3.5. Нахождение обратной матрицы

Для нахождения обратной матрицы также используется метод Гаусса с частичным выбором ведущего элемента.

Напомним, что если , то существует  такая, что , где E – единичная матрица.

 – это и есть система линейных уравнений для нахождения элементов .  содержит n² элементов, все они неизвестные.

 – это система линейных уравнений размерности  n² , но одновременно можно рассматривать как n систем линейных уравнений с одинаковой матрицей А, вектором правой части является столбец единичной матрицы, а вектором решения – столбец матрицы , т. е.

,        , где  –  столбец единичной матрицы ,;  –  столбец матрицы .

Решая эти системы линейных уравнений методом Гаусса с частичным выбором ведущего элемента, получаем столбцы , образующие матрицу . Следует отметить, что хотя мы решаем n систем линейных уравнений, но матрица у всех систем линейных уравнений одинакова, следовательно, ведущие элементы матрицы мы находим один раз.

Если же detA = 0, то при использовании метода Гаусса с частичным выбором ведущего элемента этот факт обнаружится, так как ведущий элемент будет равен нулю. Таким образом, используя метод Гаусса с частичным выбором ведущего элемента, мы либо находим обратную матрицу , либо приходим к выводу, что detA = 0.

3.6. Метод Гаусса-Жордана

Метод Гаусса-Жордана – это модификация метода Гаусса. После выполнения прямого хода в методе Гаусса-Жордана матрица преобразуется к диагональной, а не к верхней треугольной. Обратный ход в методе Гаусса-Жордана – это решение системы линейных уравнений с диагональной матрицей.

Рассмотрим пример использования метода Гаусса-Жордана.

Пример