Численные методы решения систем линейных уравнений, страница 5

Используя метод Гаусса-Жордана с частичным выбором ведущего элемента, решить систему линейных уравнений: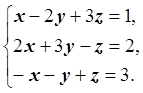

Решение

Прямой ход

Находим максимальный по модулю элемент в непреобразованном столбце и меняем местами строки. Получим:

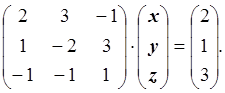
Умножим первое уравнение на (-0.5) и прибавим ко второму. Умножим первое уравнение  на (0.5) и прибавим к третьему. Получим:

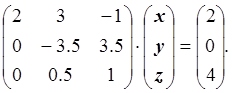
Выбираем максимальный по модулю элемент в непреобразованном столбце, он равен , поэтому перестановка строк не нужна. Теперь нам нужно занулить не только , но и . Умножим второе уравнение на 6/7 и прибавим к первому. Умножим второе уравнение на 1/7 и прибавим к третьему. Получим:

 

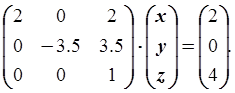
Третье уравнение умножим на (-3.5) и прибавим ко второму. Третье уравнение умножим на (-2) и прибавим к первому. Получим:

 

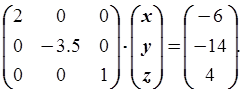
Прямой ход метода Гаусса-Жордана закончен.

Обратная подстановка

z = 4.

-3.5y = -14, следовательно, y = 4.

2x = -6, следовательно, x = -3.

3.7. Итерационные методы решения системы линейных уравнений

Эти методы не позволяют найти точное решение системы линейных уравнений за конечное число арифметических действий даже в отсутствие погрешности вычислений. С помощью таких методов строится последовательность векторов . Каждый элемент последовательности – вектор x^(k) размерности n:

.

При выполнении определенных условий последовательность векторов  сводится к точному решению системы линейных уравнений, то есть , где  – точное решение системы линейных уравнений: .

3.8. Метод итераций

Пусть ищется решение системы линейных уравнений  с невырожденной матрицей  A ().

Так как , следовательно, система линейных уравнений  имеет единственное решение.

Преобразуем систему линейных уравнений  к виду: , где  – квадратная матрица,  – вектор. Причем системы являются эквивалентными, то есть их решения совпадают. В дальнейшем мы будем рассматривать систему .

Выбирается вектор начального приближения:

.

Строится итерационный процесс:

.

Итерационный процесс прекращается при выполнении условия:

, где  – точное решение системы линейных уравнений. В этом случае  – приближенное решение системы линейных уравнений с точностью , полученное методом итераций.

Естественно, возникает ряд вопросов:

·  При каких условиях последовательность  сходится к точному решению системы линейных уравнений?

·  Как выбирать начальное приближение ?

·  Как сформулировать условия остановки итерационного процесса?

Последовательно будем отвечать на эти вопросы.

Теорема о сходимости

Пусть система линейных уравнений  имеет единственное решение. Для сходимости последовательности приближений  к точному решению системы линейных уравнений  достаточно, чтобы . При выполнении этого условия последовательность  сходится к точному решению при любом векторе начального приближения .

Оценка погрешности. Для метода итераций удается получить две оценки погрешности: априорную и апостериорную.

Априорная оценка погрешности – это оценка погрешности , которую можно получить до начала вычислений, зная только  и .

Апостериорная оценка погрешности – это оценка погрешности , которую получают, используя вычислительные приближения   и зная .

Теорема (априорная оценка погрешности)

Пусть система линейных уравнений  имеет единственное решение. Пусть . Тогда имеет место неравенство:

,   ,

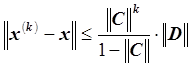где – k-е приближение, полученное методом итераций;  – точное решение системы линейных уравнений .

Отметим, что априорная оценка погрешности позволяет до вычислений оценить число шагов k, необходимых для достижения точности :

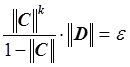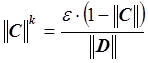,         ,  следовательно, .

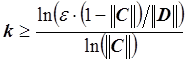Следствие. Пусть система линейных уравнений  имеет единственное решение. Пусть , тогда для числа итераций k, необходимых для достижения точности e, справедливо следующее неравенство:

.

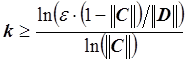Отметим, что все нормы, входящие в это неравенство, должны быть согласованы. То есть если мы выбираем первую норму матрицы С, то должны взять и первую норму вектора D. Как правило, число шагов k, полученное из этой оценки, является заметно завышенным.

Теорема (апостериорная оценка погрешности)

Пусть система линейных уравнений  имеет единственное решение. Пусть , тогда имеет место неравенство: