











Рабочая тетрадь по начертательной геометрии
1.Точки
1.1 По заданным координатам построить три проекции точек.
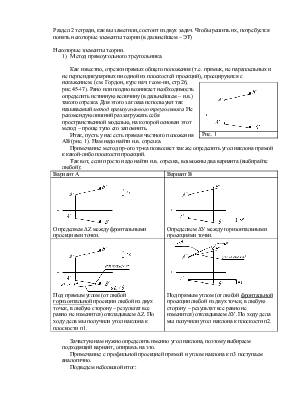
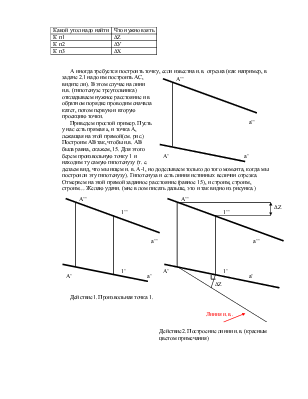
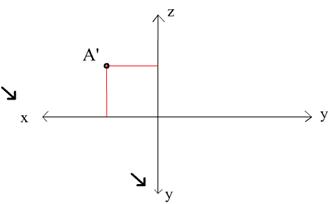
Разберем эту задачу на примере. Пусть надо построить точку А(-30, 25, 9).
 Надо обязательно запомнить,
какими координатами задается какая-нибудь проекция точки.
Надо обязательно запомнить,
какими координатами задается какая-нибудь проекция точки.
А’ , горизонтальная проекция точки А, задается координатами X,Y
A’’ , фронтальная проекция точки А, задается координатами X,Z
A’’’, профильная проекция точки А, задается координатами Y,Z
Обратите внимание на то, какие именно оси проекций нужно использовать для определения координат точки (см. рисунки)
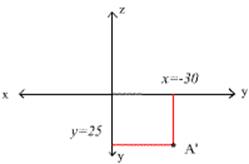
Построим точку по ее координатам.
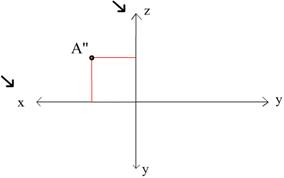
· Строим горизонтальную проекцию точки А. Для этого отмеряем координаты Х и У, т. е. -30 и 25.
·
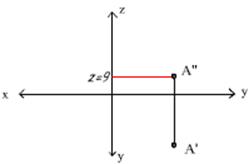 Строим фронтальную проекцию точки А, т. е. А’’. Так
как координата Х этой точки у нас уже отмерена (А’ у нас уже построена) , то
отмеряем координату Z на оси Z, равную 9. Проводим прямой отрезок от A’
до места A’’. (Эта линия называется линией связи.)
На пересечении этого отрезка и линии z=9 и будет лежать
A’’.
Строим фронтальную проекцию точки А, т. е. А’’. Так
как координата Х этой точки у нас уже отмерена (А’ у нас уже построена) , то
отмеряем координату Z на оси Z, равную 9. Проводим прямой отрезок от A’
до места A’’. (Эта линия называется линией связи.)
На пересечении этого отрезка и линии z=9 и будет лежать
A’’.
·
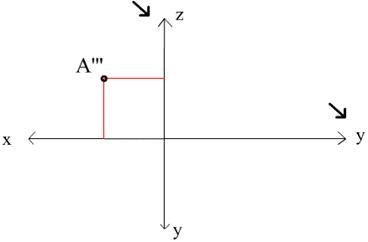
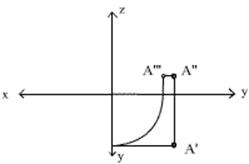 Строим профильную проекцию точки А – строим A’’’: переносим Y=25 на другую ось Y (примечание: при переносе
координаты c Уп2 на Уп3 линию
связи можно проводить тремя способами: или циркулем, как четвертинку
окружности, или линией под углом 45 градусов, или как показано на третьем
рисунке). А ось Z у нас одна! И
координата Z равна 9. Это
значит, что A’’’ будет лежать на одной линии связи с A’’.
Строим профильную проекцию точки А – строим A’’’: переносим Y=25 на другую ось Y (примечание: при переносе
координаты c Уп2 на Уп3 линию
связи можно проводить тремя способами: или циркулем, как четвертинку
окружности, или линией под углом 45 градусов, или как показано на третьем
рисунке). А ось Z у нас одна! И
координата Z равна 9. Это
значит, что A’’’ будет лежать на одной линии связи с A’’.
А вообще, можно не париться, а
тупо отмерить 25 на Уп3 и 9 на Z и
построить A’’’. Но это будет тупо, да к 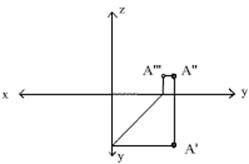 тому же линию
связи строить придется все равно.
тому же линию
связи строить придется все равно.
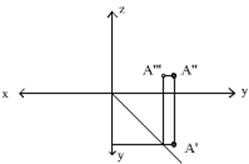
Таблица для определения октант.
|
X |
Y |
Z |
|
|
I |
+ |
+ |
+ |
|
II |
+ |
- |
+ |
|
III |
+ |
- |
- |
|
IV |
+ |
+ |
- |
|
V |
- |
+ |
+ |
|
VI |
- |
- |
+ |
|
VII |
- |
- |
- |
|
VIII |
- |
+ |
- |
Вас обязательно спросят, в каком октанте расположена точка! Для этого вам придется запомнить таблицу октант, т. к. представлять в уме, где находится точка в пространстве, очень долго. Глазунов, например, сразу пошлет вас на три буквы. Тем не менее, запомнить ее очень просто:
1) Первые четыре октанты отличаются от последних четырех только тем, что в первом столбце сверху стоят четыре плюса, а снизу – четыре минуса.
|
|
2) Второй, средний столбец в каждой половине состоит из плюса, двух минусов посередине и снова плюса.
|
+ |
|
- |
|
- |
|
+ |
Легко запомнить: средний столбец – минусы посередине.
3) В третьем столбце просто чередуются два плюса/два минуса (чем-то это напоминает заполнение таблицы истинности единичками и ноликами).
|
+ |
|
+ |
|
- |
|
- |
2. Линии.
Раздел 2 тетради, как вы заметили, состоит из двух задач. Чтобы решить их, потребуется понять некоторые элементы теории (в дальнейшем – ЭТ)
Некоторые элементы теории.
1) Метод прямоугольного треугольника.
|
|
|
Рис. 1 |
Как известно, отрезки прямых общего положения (т.е. прямых, не параллельных и не перпендикулярных ни одной из плоскостей проекций), проецируются с искажением. (см. Гордон, курс нач. геом-ии, стр.26, рис.45-47). Рано или поздно возникает необходимость определить истинную величину (в дальнейшем – и.в.) такого отрезка. Для этого за глаза используют так называемый метод прямоугольного треугольника. Не рекомендую лишний раз загружать себя пространственной моделью, на которой основан этот метод – проще тупо его запомнить.
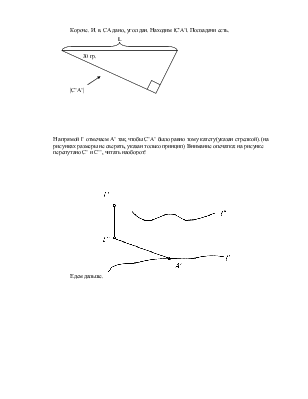
Итак, пусть у нас есть прямая частного положения АВ (рис. 1). Нам надо найти и.в. отрезка.
Примечание: метод пр-ого тр-ка позволяет так же определить угол наклона прямой к какой-либо плоскости проекций.
Так вот, если просто надо найти и.в. отрезка, возможны два варианта (выбирайте любой):
|
Вариант А |
Вариант В |
|
Определяем ∆Z между фронтальными проекциями точки. |
|
|
Под прямым углом (от любой горизонтальной проекции любой из двух точек, в любую сторону – результат все равно не изменится) откладываем ∆Z. По ходу дела мы получили угол наклона к плоскости п1. |
Под прямым углом (от любой фронтальной проекции любой из двух точек, в любую сторону – результат все равно не изменится) откладываем ∆У. По ходу дела мы получили угол наклона к плоскости п2. |
Зачастую нам нужно определить именно угол наклона, поэтому выбираем подходящий вариант, опираясь на это.
Примечание: с профильной проекцией прямой и углом наклона к п3 поступаем аналогично.
Подведем небольшой итог:
|
Какой угол надо найти |
Что нужно взять |
|
К п1 |
∆Z |
|
К п2 |
∆У |
|
К п3 |
∆X |
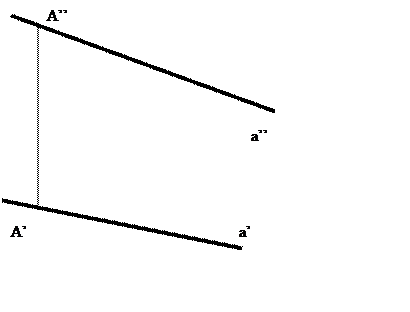 А иногда
требуется построить точку, если известна и.в. отрезка (как например, в задаче
2.1 надо им построить АС, видите ли). В этом случае на лини и.в. (гипотенузе
треугольника) откладываем нужное расстояние и в обратном порядке проводим
сначала катет, потом первую и вторую проекцию точки.
А иногда
требуется построить точку, если известна и.в. отрезка (как например, в задаче
2.1 надо им построить АС, видите ли). В этом случае на лини и.в. (гипотенузе
треугольника) откладываем нужное расстояние и в обратном порядке проводим
сначала катет, потом первую и вторую проекцию точки.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.