Точки. Линии. Теорема о частном случае проецирования прямого угла (Рабочая тетрадь по начертательной геометрии), страница 3

Вот собственно и все. С задачей 3,1 справитесь, вникнув в написанное выше.(или просто перерисуйте).

Задача 3,2

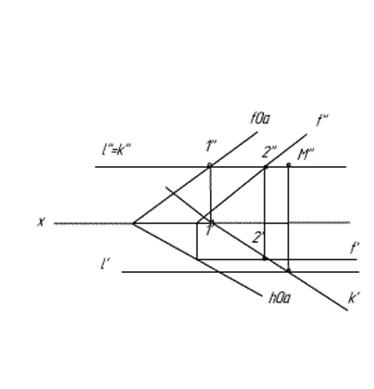
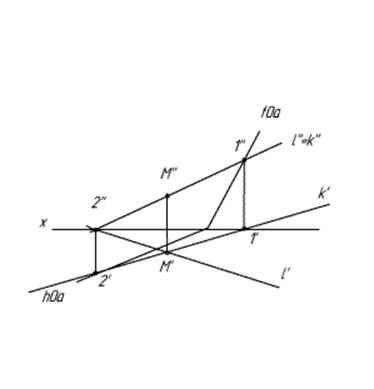
1) Вот так:строим следы прямых.

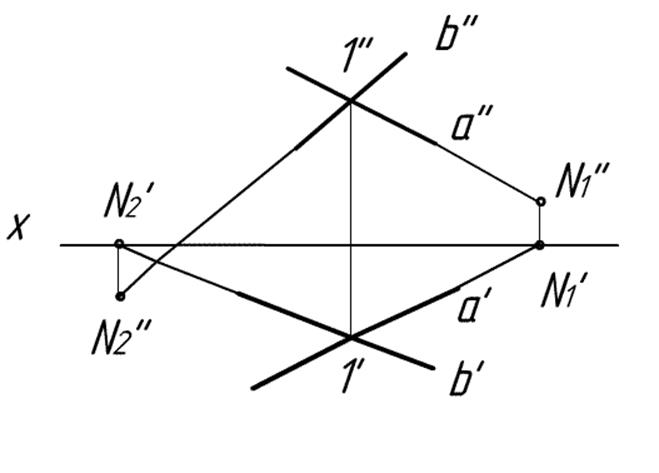
2)  Вот:

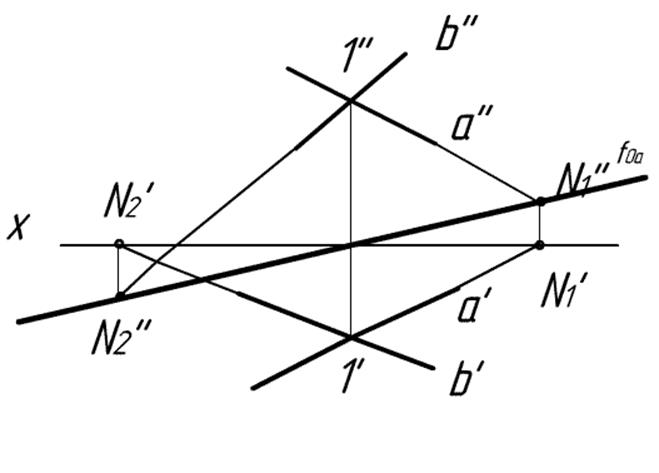
3)Строим горизонталь h по двум точкам 2 и 3:

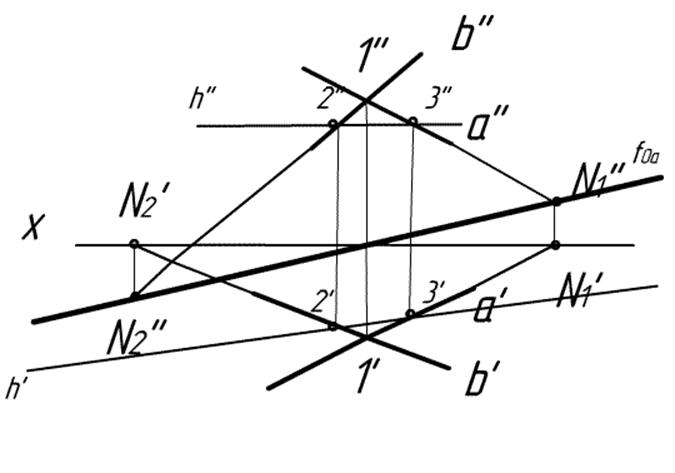
4)||-но h’ проводим h0α. Все!

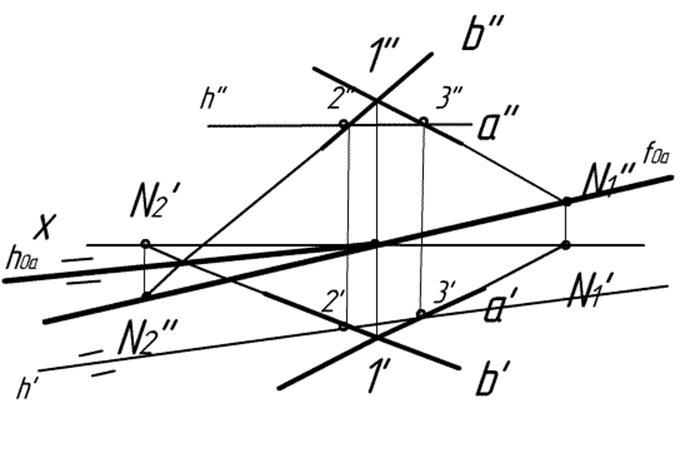
А в задаче 3,3 всегда получается каша. Сделайте ее сами. Она довольно проста на самом деле.

4. Проецирующие плоскости.

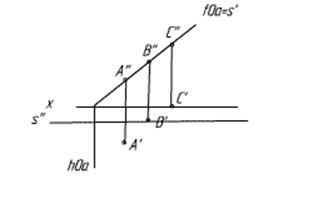
4,1 Собственно, проецирующая плоскость – плоскость, перпендикулярная к плоскости проекций. Если ее задать следами, то один из них будет перпендикулярен к оси, а ежели ее задать двумя прямыми, то они будут конкурировать (т.е. проекции сольются в одну, как у плоскости, заданной прямыми а и в на рисунке). У нее есть свойство собирательности (т.е. все проекции точек собираются на один след, см. рис).

Линия ската – линия наибольшего наклона плоскости к п1. Представьте себе какую-нибудь плоскость, которая наклонена к п1. Положим на нее шарик. Он покатится по прямой траектории. Эта прямая и будет линией ската.

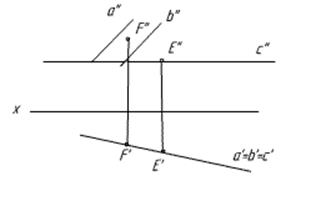
В общем, проекции A’’, B’’, C’’ пойдут на след. Линия ската пойдет параллельно оси через точку B. Вторая проекция линии ската «соберется» на след. F’ и E’ «соберутся» прямиком на a’=b’, туда же «соберется» гориз. проекция линии наиб. наклона к пл-ти п2. Фронтальная пройдет || - но оси через E’’. Все.

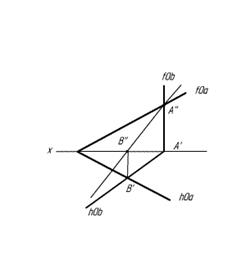
4,2 Зачем париться, вспоминая частные случаи методов нахождения точки встречи прямой и плоскости,  гораздо проще запомнить всего один и применять его везде. Он является довольно легким и называется МЕТОД КОНКУРИРУЮЩИХ ПРЯМЫХ; тем более вам он очень понадобится в дальнейшем (хотя, конечно, есть и другие методы, но по-моему, этот самый легкий).

Алгоритм:

1)Заключаем заданную прямую в конкурирующую прямую, принадлежащую плоскости.(я всегда называю ее k, хотя это не принципиально). Этот пункт на чертеже выглядит просто: приписываем l’≡k’ или l’’≡k’’. Приписывать в обязательном порядке!

2)Строим вторую проекцию k по двум точкам.

3) Точка пересечения прямой k с данной – искомая.

Вот как это выглядит:

Дано: Найти точку встречи прямой l c плоскостью α(a,b)

Пункт 1. Просто пишем l’’≡k’’

Пункт 2. Строим k’ по двум точкам (ведь k принадлежит плоскости)

Пункт 3. Смотрим, где k’ пересеклось с l’. Назовем ее Ритой (шутка, назовем ее M’). Поднимаем вверх проекционную связь, получаем M’’.

Если плоскость задана следами, поступаем аналогично: заключаем, берем любые две понравившиеся точки, строим, находим. Примечание: удобнее брать точки  на следе и на оси.

В принципе в задаче 4,2 рассуждайте так же: куда проецируется конкурирующая прямая? Где же искомая точка? И вы без проблем все построите.

4,3 Задача заключается в нахождении двух точек, принадлежащих обеим плоскостям. Так, на первой картинке взята точка В: В’ на пересечении следов => B’’ на оси. Точка А аналогично.

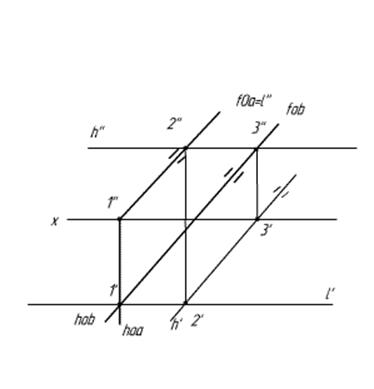Во втором случае берем точку 1, как и в предыдущем случае. Но где же нам взять вторую точку? Из рисунка мы видим, что она как бы стремится к бесконечности. Задача решается так: проводим горизонталь h плоскости β. Горизонтальная проекция горизонтали будет параллельна h0β. Строим ее. Общая точка будет лежать на фронтальной проекции горизонтали и в плоскости α  одновременно.  Это – точка 2, фронтальная проекция которой будет лежать на пересечении h’’ и f0α. Горизонтальная проекция точки 2 лежит на h’. Осталось построить искомую прямую, проходящую через точки 1 и 2. Здесь она получила имя l.

5, прямая и плоскость.

5,1 Используйте метод конкурирующих прямых и радуйтесь!

5,2 Дерзайте: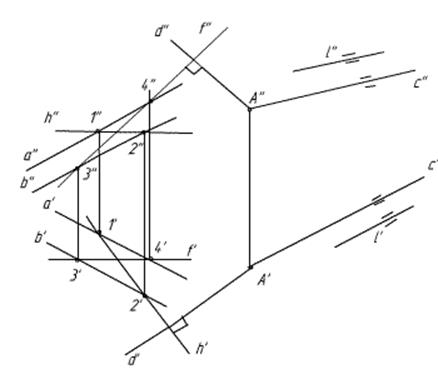

Здесь проще всего задать искомую плоскость двумя прямыми, пересекающимися в точке А. Пусть это будет плоскость α(с,d).

1)Прямая || - а плоскости, если она ||-а какой-нибудь прямой в этой плоскости. Поэтому строем прямую с || - о прямой l: с’||l’, c’’||l’’,разумеется, через точку А.