Точки. Линии. Теорема о частном случае проецирования прямого угла (Рабочая тетрадь по начертательной геометрии), страница 2

Приведем простой пример. Пусть у нас есть прямая a, и точка А, лежащая на этой прямой(см. рис.) Построим АВ так, чтобы и.в. АВ была равна, скажем, 15. Для этого берем произвольную точку 1 и находим ту самую гипотенузу (т. е. делаем вид, что мы ищем и. в. А-1, но доделываем только до того момента, когда мы построили эту гипотенузу). Гипотенуза и есть линия истинных величин отрезка. Отмеряем на этой прямой заданное расстояние (равное 15), и строим, строим, строим… Желаю удачи. (мне в лом писать дальше, это и так видно из рисунка.)

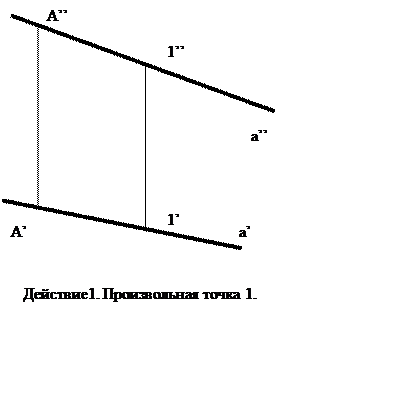
Нетрудно догадаться, что если нам даны две из  трех величин (например, ∆Z и и.в., или может быть какой-нить угол), то третью из прямоугольного треугольника мы легко найдем.

Теорема о частном случае проецирования прямого угла.

Собственно, теорема звучит так:

Если одна из сторон угла параллельна плоскости проекций, а другая не перпендикулярна этой плоскости, то угол проецируется на эту плоскость в истинную величину. (см. Гордон, стр. 38, рис. 89)

Никогда не следует забывать про вторую часть теоремы про «другая не перпендикулярна этой плоскости».

В общем можно сказать, что если у нас прямая частного положения(горизонталь или фронталь), то теорема будет справедлива, правда, с учетом некоторых оговорок.(подумайте, каких).

Итак, приступим. С задачей 2,1 вам все должно быть ясно (не зря же я старался, примеры приводил!). Едем дальше.

2,2 Вертолет, летит… Тьфу! Нехорошая (хотя, для кого как) задача, и в условие сразу не въедешь… Был засечен. Локатором. В точке. Угол места, расстояние до локатора… Найти положение.

Короче. И. в. СА дано, угол дан. Находим |С’A’|. Ползадачи есть.

На прямой l’ отмечаем А’ так, чтобы С’A’ было равно тому катету(указан стрелкой). (на рисунках размеры не сверять, указан только принцип) Внимание опечатка: на рисунке перепутано С’ и C’’, читать наоборот!

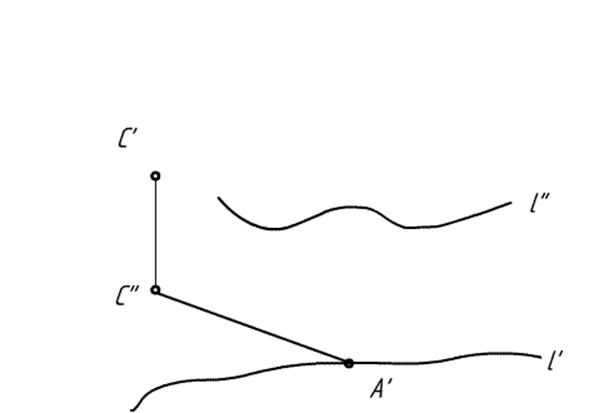
Едем дальше.

Продолжаем линию связи от А’. Под углом 30 градусов проводим линию из точки C’’. Получаем А’’ . Задача решена.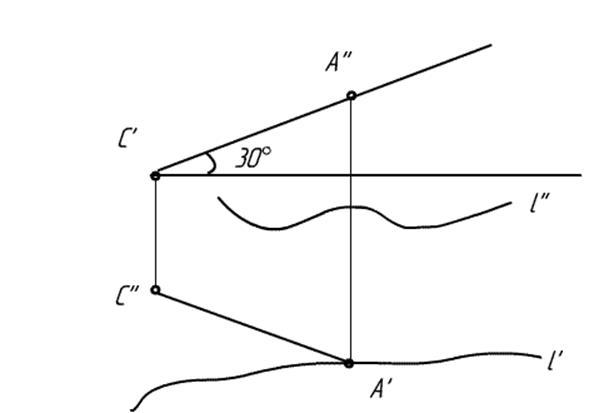

3. Плоскость

Рис 2

Рис. 3

Необходимая теория.

Плоскость можно задать по-разному, в том числе и следами. Следы плоскости – линии пересечения плоскости с плоскостями проекций. На рис. 2 плоскость α задана следами: горизонтальным h0α и фронтальным f0α.

Рис. 5

Рис 4

Пусть некоторая точка лежит в плоскости, заданной следами. Запомните правило: фронтальная проекция точки на фронтальном следе – горизонтальная проекция на оси(и наоборот: если штрих на оси, то два штриха на следе), горизонтальная проекция на горизонтальном следе – вторая проекция на оси(и наоборот).(рис. 3)

Точка лежит в плоскости, если она лежит в какой-нибудь прямой этой плоскости. Это условие нам понадобится, чтобы построить вторую проекцию точки. Если плоскость задана следами, то горизонтальная проекция любой горизонтали, лежащей в этой плоскости, будет параллельна горизонтальному следу, а фронтальная фронтали – фронтальному (простите за каламбур)(рис. 4). Таким образом, если дана одна проекция точки, принадлежащей плоскости, заданной следами, мы всегда можем провести горизонталь или фронталь и построить вторую (рис. 5). На рисунке 5 была дана A’’. Мы провели проекцию горизонтали h’’ через эту точку. По правилу « “ 1’’ ” на следе -> “  1‘  “ на оси» построили точку 1. Через эту точку провели h’ ||  h0α. Продолжили линию связи, построили А’’. С точкой B – аналогично.

При выполнении задачи 3.1 помните, что если плоскость задана прямой и точкой, или двумя параллельными прямыми, или следами, мы всегда можем перезадать ее двумя пересекающимися прямыми, просто проведя оные. Это очень удобно для построения недостающих проекций точек.  Алгоритм такой: строим прямую через точку, с помощью точек пересечения этой прямой с двумя прямыми, которыми задана плоскость, строим вторую проекцию этой прямой. Вторые проекции точек будут лежать на только что построенной проекцией прямой.