2) Прямая перпендикулярна плоскости, если она перпендикулярна каким-нибудь двум пересекающимся прямым в этой плоскости. Как же построить такую прямую? Да элементарно. Вспоминаем теорему о частном случае проецирования прямого угла(см. раздел 2). Ага, понятно. Проводим горизонталь h и фронталь f, по двум точкам строим вторые их проекции. И через точку А фигачим d’ перпендикулярно h’, d’’ перпендикулярно f’’. Все!
5.3 Легендарная задача с самолетами… Опять ни фига не понятно… Но ничего.
Сию
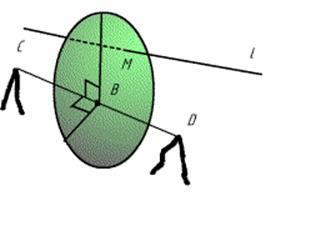
задачу переформулируем так: на прямой l найти точку, равноудаленную от точек C и D.
Да нет проблем!
Представим, как это дело выглядит в пространстве. Очевидно, что равноудаленная точка будет находится в плоскости, проходящей через центр отрезка CD – через точку В и перпендикулярную к прямой СD.(см. рис.) А точка встречи этой плоскости с прямой l и будет искомая.
Итак,
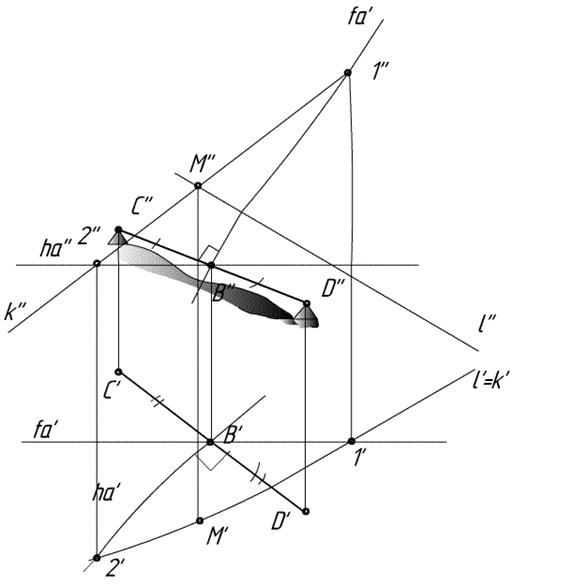
алгоритм:
1) Отметим точку B в центре отрезка CD.
2) Проведем вспомогательную плоскость α(h.f) перпендикулярно к CB: h’┴C’D’, f’’┴C’’D’’
3) Находим точку пересечения плоскости α(h.f) с прямой l методом конкурирующих прямых, который описан выше. Примечание: конечно же, можно использовать любой другой метод.
4) Все!!!!! На рисунке вышли кривоватые линии, но остальное – правда!
5,4 Чтобы построить этот долбанный квадрат, нам не хватает точек В,С и D. Но зато у нас есть прямая, на которой лежат точки B и C, и это очень хорошо. Просто так, т. е. ┴-но l’, AB мы построить не можем – не действует теорема о частном случае проецирования прямого угла. Как же нам построить точку В? Да легко! Через точку А проведем плоскость, перпендикулярную к прямой l и найдем точку встречи этой прямой с этой плоскостью. Это по ходу и будет та самая точка В. Ура!!! Точку В нашли!
Ну нашли мы ее, что дальше – то? Как найти точку С? Вот тут наступает время вспомнить, что это – квадрат, а раз это квадрат, то у него все сторонни равны. Мы нашли B, у нас была А, и теперь нам надо всего лишь найти и.в. АВ и отложить на прямой l отрезок BC так, чтобы и.в. ВС была равна и.в. АВ.(см. раздел 2 в теории).
Теперь время вспомнить, что стороны квадрата попарно параллельны, и следовательно и проекции сторон квадрата тоже попарно параллельны. Улыбаясь, достраиваем квадрат и едем дальше.
5,5 Ну вот, опять пошли всякие трубопроводы… Нет чтобы по-русски все написать! Ладно, даю алгоритм:
1) На прямой l берем произвольную точку Е.
2)Через точку Е проводим прямую р ┴α(ABCD): p’┴h’, p’’┴f’’,
3)Строим точку F так, чтобы и.в. EF=d/2 (радиусу трубопровода).(см. линии)
4) Через точку F проводим i||l.: i’||l’, i’’||l’’
А теперь берем пару конкурирующих точек, сравниваем их координаты, определяем видимость. Вперед, за дело!
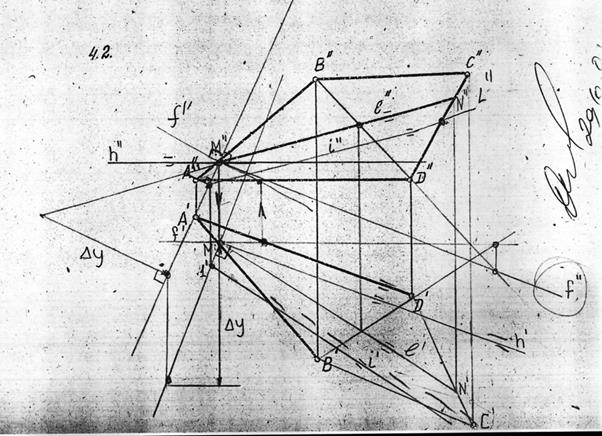
Рисунок взят с сайта www.BOEHMEX.ru Вроде что-то похожее они там намудрили… Хотя не знаю, по-моему каша какая-то. Люди, не берите точку в пересечении стороны и l, берите ПРОИЗВОЛЬНО, например справа., чуть левее N’’, и получится значительно красивей. И диагонали на фиг нужны, по-моему. Используйте параллельность сторон AD и BC.
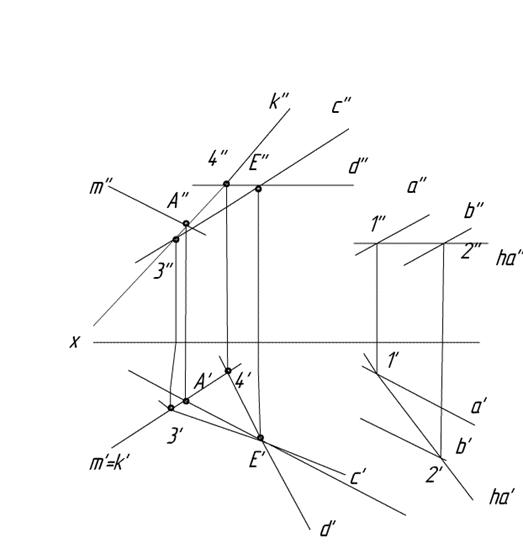
5.6 Алгоритм:
1) Через В проводим β(с,d)||α(a,b): c||a следовательно c’||a’, c’’||a’’, d||hα => d’|| hα’, d’’|| hα’’ (Горизонталь hα естественно тоже надо провести)
2) Ищем Е - (.)-у встречи прямой m с плоскостью β(с,d) (метод конкурирующих прямых, приведен выше).
3) ЕА – искомая прямая. ВСЕ!
6,1 Построить линию пересечения плоскостей.
Первая часть задачи делается аналогично задаче 5,1.
Во второй части задачи берем единственную нужную нам точку – точку 1, фронтальная проекция которой лежит на пересечении f0α и f0β, а горизонтальная – на оси. Пусть искомая прямая – l. Тогда l’’ пройдет через 1’’ ||-о оси. l’ пройдет ||-о h0α.
В третьей части… Да что там объяснять, срисуйте и все. Примечание: прямые 2-4 и 1-3 проведены от балды ||-о оси.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.