Определение координат точек. Октанты в начертательной геометрии

ТОЧКИ

Надо обязательно запомнить, какими координатами задается какая-нибудь проекция точки.

А’ , горизонтальная проекция точки А, задается координатами X,Y. Примечание: На рисунке видим, что оси У у нас якобы две. Для А’ берем ту, которая перпендикулярна оси Х. (рис. 1)

A’’ , фронтальная проекция точки А, задается координатами X,Z (рис. 2).

A’’’, профильная проекция точки А, задается координатами Y,Z. Примечание: для A’’’ следует взять ту ось У, которая перпендикулярна оси Z. (рис. 3)

Обратите внимание на то, какие именно оси проекций нужно использовать для определения координат точки (см. рисунки)

1)  Определение координат точек.

Пусть вам даны две какие-нибудь проекции точки. Как определить их координаты? Очень просто. Начнем издалека. Как известно, любая точка определяется в пространстве тремя координатами: X, Y и Z. Это понятно.

Если вам дана A’, то мы автоматически сможем сказать, какие у этой точки будут координаты Х и У – см. рис. 1. Обратите внимание на знак координаты!  Знак определяется в зависимости от того, в какую сторону направлена ось. На рис. 4 очевидно, что координата X точки А отрицательна, а координата У положительна. Повторюсь: мы взяли именно эту ось У, так как она перпендикулярна оси Х, а A’ «зависит» от координаты X. Если бы мы искали координату У с помощью профильной проекции точки (A’’’), то мы бы взяли ось, перпендикулярную оси Z, так как A’’’  «зависит» от координаты Z. Иными словами, оси, по которым определяются две координаты проекции, не могут лежать на одной линии.

Пусть к тому же нам дана A’’. Это нам дает координаты X (которая равна этому же иксу, взятому у A’ -  отсюда и следует, что A’ и A’’ расположены на вертикальной линии связи)  и Z – координату, которой не было (и никогда не будет) у A’. (см. рис. 2). Вот и все – мы нашли три координаты точки А всего по двум проекциям.

2)  Октанты.

В начертательной геометрии существует такое понятие, кок октант. Что такое октант?

Три оси – x,y и z делят пространство на 8 равных частей. Каждая из таких частей и называется октантом.

Чтобы по знакам точки определить, в какой октанте она расположена, достаточно запомнить довольно простую таблицу. Вот она.

Запомнить ее очень просто:

1) Первые четыре октанты отличаются от последних четырех только тем, что в первом столбце сверху стоят четыре плюса, а снизу – четыре минуса.

2) Второй, средний столбец в каждой половине состоит из плюса, двух минусов посередине и снова плюса.

Легко запомнить: средний столбец – минусы посередине.

3) В третьем столбце просто чередуются два плюса/два минуса (чем-то это напоминает заполнение таблицы истинности единичками и ноликами).

3)  Нахождение третьей проекции по двум заданным.

Чаще всего в такой задаче недостает либо A’, либо A’’’. Напишем алгоритм для такой задачи. Пусть у нас имеется A’’ и A’ (A’’’). Далее все, что касается A’’’, указано в скобках.

1)  Ведем от A’(или A’’’) горизонтально (вертикально) линию связи по направлению к оси У.

2)  Продолжаем проводить линию связи: строим четверть  окружности от одной оси У к другой. (можно и не окружность, а прямую линию под углом 45 гр.) Не ошибитесь: она может быть либо с этой стороны: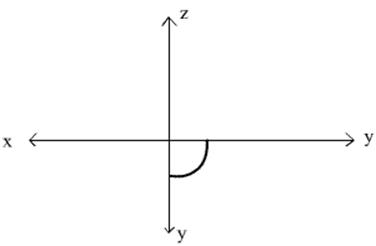

Либо с этой стороны:

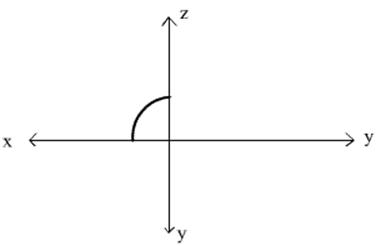
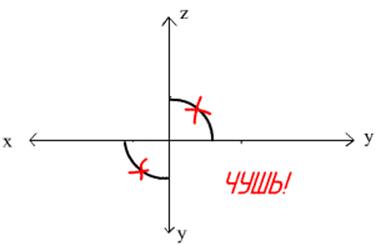
С двух других сторон – она быть не может, хоть ты тресни.

3)Продолжаем вести линию связи. Ведем ее вертикально (горизонтально) в направлении к A’’. Горизонтально ( вертикально) от A’’ проводим линию по направлению к той линии, которую мы тока-тока построили, до пересечения с ней. На пересечении и будет лежать A’’’ (A’).

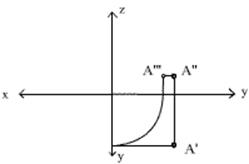
Если недостает A’’: проводим от А’ вертикальную, а от A’’’ горизонтальную линии. Там, где они пересекутся, и будет A’’.

Иногда бывают частные случаи, когда какая-нибудь из проекций на оси. В этом случае какая-то координата точки будет равна нулю. Строим третью проекцию по координатам, взятым от двух исходных.