Ответы на вопросы зачета по дисциплине "Ракетно-космическая техника" (Античные ракетные системы. Развитие ракетной техники в древнем Китае. «Лунная гонка» 60-х годов и её воздействие на развитие ракетной техники), страница 10

3-е – движение ракеты как ТВ. тела вокруг её ЦМ

4-5 и 5-е – скорость ЦМ в земной СК

6-е и 7-е – изменение угла отклонения газовых рулей

- сила веса ракеты, Р – сила тяги, Q – лобовое сопротивление (лежит в пл-ти местного гор-та),  – проекция газодинам. силы на руль,  – перпенд. пл-ти местного гор-та.

5. Основные уравнения движения баллистической ракеты (РН)  на пассивном участке

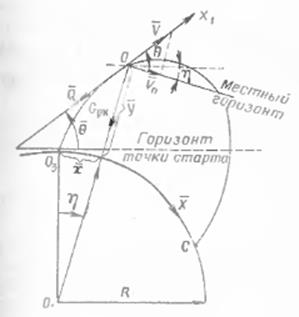
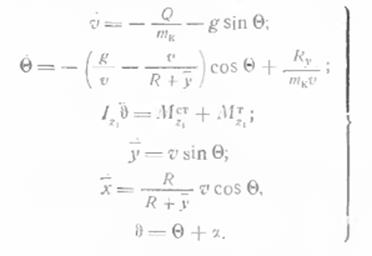
Угол атаки = 0, криволин. СК.

6. Формула Мещерского и её вывод

Пусть относительно некоторой неподвижной системы координат движется точка переменной массы . В момент времени t абсолютная скорость этой точки , а количество движения -  .

Предположим, что за время  точка массы отделяет частицу массы , абсолютная скорость которой равна  .

Вмомент времени количество движения системы (точка, отбрасывавшая массу, и отделившаяся частица) будет. .Движение точки переменной массы происходит под действие внешних сил, равнодействующая которых . Тогда изменение количества движения рассматриваемой системы за время

Пренебрегая слагаемыми второго порядка малости , разделив обе части равенства на и затем перейдя к пределу при  —> 0, получим

где  – относительная скорость   отделяющейся   частицы, - расход отбрасываемой массы в единицу времени. Тогда

Слагаемое имеет размерность силы — эта добавочная сила возникает вследствие отделения частиц от массы  и называется реактивной силой.

После этого уравнение принимает окончательный вид:

Это уравнение принято называть уравнением И.В. Мещерского: для любого момента времени t при движении точки переменной массы произведение массы точки на ее ускорение равно геометрической сумме равнодействующей всех внешних сил и дополнительной реактивной силы .

7. Формула силы тяги и её вывод одним из существующих методов (методом

 закрепления ракеты на стенде)

При работе двигателя закрепленной ракеты в стенде возникают силы, противодействующие тяге двигателя. Так как ракета неподвижна, ускорение равно нулю и уравнение движения точки переменной массы принимает вид:

, где

S_a – площадь сечения на срезе сопла, w - скорость истечения продуктов сгорания, p_a – давление продуктов сгорания на выходе из сопла, а р – давление окружающей среды. Так как R=P, то

но так как имеют место разные условия обтекания, а так же ракеты летают на разных высотах, то будем считать p_h – барометрическим давлением окружающей среды на данной высоте:

Обычно пустотная тяга отличается от стартовой примерно на 10-15%.

8. Влияние площади поперечного сечения сопла на силу тяги

Смотри седьмой вопрос)))

9. Формула Циолковского и её вывод

Идеальная скорость одноступенчатой ракеты. Скорость, развиваемая ракетой в безвоздушном пространстве в отсутствии гравитационных сил, называется идеальной скоростью .

Для определения идеальной скорости можно воспользоваться уравнением Мещерского, считая, что равнодействующая внешних сил (гравитационных и аэродинамических) равна 0. Тогда, с учетом того, что отбрасывание части собственной массы - рабочего тела - происходит со скоростью, называемой эффективной скоростью истечения(определяемой с учетом конструкции сопла ракетного двигателя), уравнение Мещерского можно записать как

откуда

Считая, что эффективная скорость истечения постоянна, а начальная скорость ракеты равна 0, проинтегрируем это уравнение с разделенными переменными. В результате получаем соотношение:

где - стартовая масса ракеты,  — текущее значение массы ракеты.

Это соотношение было впервые получено Циолковским применительно к полету ракеты и позднее по предложению технического совета РНИИ получило название «формула Циолковского».

Отношение принято называть относительной массой ракеты, показывающей, какую долю стартовой массы сохранит ракета к рассматриваемому моменту времени. К моменту выключения двигателя это отношение принимает значение   - относительная конечная масса ракеты (иначе - относительная масса конструкции, поскольку можно считать, что в момент выключения двигателя топливо ракеты израсходовано полностью). Поэтому наибольшая (идеальная) скорость ракеты