Предварительный расчет параметров стартового сверхкритического порохового аккумулятора давления (ПАД). Внутрибаллистический расчет параметров стартового сверхкритического ПАД. Параметры запуска объекта с использованием сверхкритического ПАД, страница 21

Среди дифференциальных уравнений отсутствует диффиренциальное уравнение для определения давления в КС (вместо этого уравнения для расчета давления использовано алгебраическое соотношение – уравнение состояния Клапейрона-Менделееева). Соответствующее дифференциальное уравнение при необходимости может быть получено путем диффиринцирования уравнения состояния.

3.6.2. Определение параметров в газовом объеме установки

Для расчета величины давления в газовой полости установки используется замыкающее соотношение в форме уравнение состояния Клапейрона Менделеева:

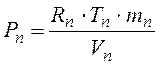
Дифференциальное уравнение для определения доли продуктов сгорания заряда в смеси газов, заполняющих полость толкателя:

;

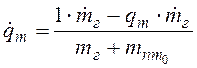Соотношения для определения параметров газовой смеси в объеме установки:

;

;

;

;

Дифференциальное уравнение для определения массы газов, вытекших через кольцевой зазор между объектом и установкой в окружающую среду. Выражения аналогичные используемым для определения расхода из КС. В приведенных ниже формулах вместо значения  используется значение

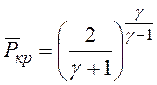 - критический перепад давлений;

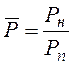 - текущий перепад давлений;

если , реализуется сверхкритический режим истечения, и расход равен

;

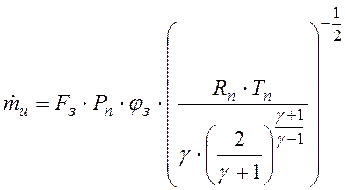если , реализуется докритический режим истечения, и расход равен

;

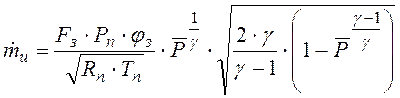До момента раскрытия зазора перепадом давления () или до начала движения объекта расход равен нулю.

Дифференциальное уравнение для определения массы смеси газов в газовом объеме установки:

;

Дифференциальное уравнение для определения температуры смеси газов в объеме установки:

.

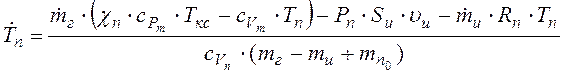Дифференциальное уравнение для определения текущей величины газового объема установки

.

значение текущего объема полости может быть получено по размерам и известному в каждый момент времени перемещению объекта. Модель, описывающая параметры в газовой полости толкателя включает в себя пять дифференциальных уравнений. Дополним ее начальными условиями интегрирования:

3.6.3. Определение кинематических параметров движения объекта до момента выхода из установки

Для определения кинематических параметров движения объекта решаются два дифференциальных уравнения.

Дифференциальное уравнение для определения скорости движения объекта в установки (проекция уравнения движения на продольную ось объекта записана для случая вертикального запуска объекта):

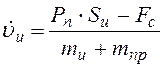, где 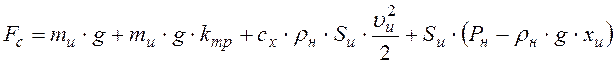 - суммарная сила сопротивления, включающая в себя учет силы тяжести, силы трения, силы лобового сопротивления и силы сопротивления за счет внешнего давления.

Дифференциальное уравнение для определения пути, пройденного объектом в установке:

.

Т.о. в данном параграфе представлена математическая модель расчета параметров запуска объекта с использованием ПАД, реализованная в программе «А4-BS».