Предварительный расчет параметров стартового сверхкритического порохового аккумулятора давления (ПАД). Внутрибаллистический расчет параметров стартового сверхкритического ПАД. Параметры запуска объекта с использованием сверхкритического ПАД, страница 14

3.  Индивидуальные исходные данные;

4.  Распечатка файла результатов, полученного по данным предварительного расчета;

5.  Распечатка файла результатов, полученного по уточненным данным;

6.  Графики зависимостей от времени по предварительным и уточненным данным (одноименные функции строятся на одном рисунке);

7.  Таблицы и графики по результатом исследования влияния факторов;

8.  Выводы.

2.6. Математическая модель внутрибаллистических процессов

В данном параграфе приводится совокупность соотношений (алгебраические соотношения и дифференциальные уравнения), реализованные в программе «A4 BR» для математического описания решаемой задачи. Соотношения записаны в том порядке, в котором они используются в программе.

Замыкающее соотношение (уравнение состояния Клапейрона Менделеева) для расчета величины давления в камере сгорания:

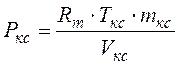
Расчет текущей величины поверхности горения вкладыша (геометрическая задача):

. В программе реализовано решение геометрической задачи, позволяющей рассчитать площадь горения одиночной шашки (или набора одинаковых шашек) и моноблока с «равномерным» расположением одинаковых сквозных каналов. Расчет производится по известным начальным размерам вкладыша и текущему значению сгоревшей толщины вкладыша. После разгорания каналов до взаимного соприкосновения считается, что поверхность горения равно нулю (догорание вкладыша не учитывается);

Дифференциальное уравнение для определения массы газа, вытекшего из КС. Текущая величина расхода вычисляется в зависимости от режима истечения:

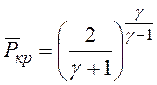 - критический перепад давлений;

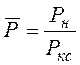 - текущий перепад давлений;

если , реализуется сверхкритический режим истечения, и расход равен

;

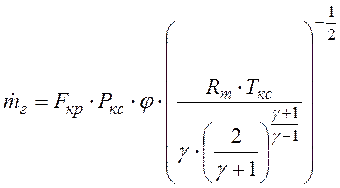если , реализуется докритический режим истечения, и расход равен

;

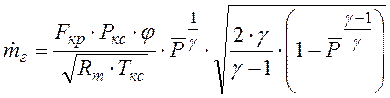в том случае, если , расход из КС равен нулю . До момента прорыва заглушки соплового блока расход также равен нулю. При выполнении заданных требований данной работы КС все время (от  до ) работает на сверхкритическом режиме истечения;

Дифференциальное уравнение для определения сгоревшей толщины свода вкладыша. Для определения линейной скорости горения используются два степенных и один линейный законы скорости горения. Каждый из законов работает в определенном интервале давлений в КС, которые задаются в исходных данных:

 - степенной закон скорости горения;

 - линейный закон скорости горения;

в том случае, если величина давления в КС не принадлежит ни одному из интервалов заданных законов, скорость горения равна нулю .

Дифференциальное уравнение для определения величины свободного объема КС. Скорость изменения объема записывается следующим образом:

;

Дифференциальное уравнение для определения сгоревшей массы вкладыша КС. Газоприход продуктов сгорания вкладыша в камеру сгорания определяется следующим образом:

;

Дифференциальное уравнение для определения массы газов в свободном объеме камеры сгорания:

;

Вообще-то, это уравнение является избыточным для решения задачи определения внутрибаллистических параметров КС, т.к. текущая масса газов в КС может быть получена из алгебраического соотношения: .

Дифференциальное уравнение для определения температуры газов в КС. Из закона сохранения энергии может быть получено выражение для скорости изменения температуры в КС:

.

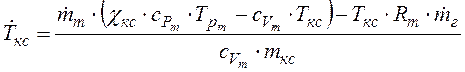Записанная модель включает в себя шесть обыкновенных дифференциальных уравнений первого порядка. Дополним ее начальными условиями интегрирования: