Алгебраический многочлен ![]() -й
степени
-й
степени
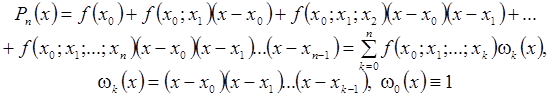 (2.7.1)
(2.7.1)
называется интерполяционным
многочленом Ньютона с разделенными разностями. Очевидна аналогия формулы (2.7.1) с формулой Тейлора. Действительно, так как по теореме 2.7 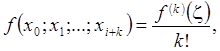 то
то 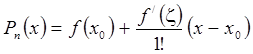
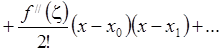 Формулы
подраздела 2.4о погрешности интерполяции
Формулы
подраздела 2.4о погрешности интерполяции 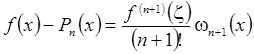 в
точке
в
точке ![]() , не являющейся узловой, можно уточнить
следующим образом:
, не являющейся узловой, можно уточнить
следующим образом: ![]() (2.7.2)
(2.7.2)
В практическом плане формула
(2.7.1) обладает рядом преимуществ перед формулой Лагранжа. Если, например, по
каким-либо причинам необходимо увеличить степень интерполяционного многочлена
на единицу, добавив в таблицу еще один узел ![]() , то при
использовании формулы Лагранжа это приведет не только к увеличению числа
слагаемых, но и к необходимости вычислять каждое из них заново. В то же время
для вычисления
, то при
использовании формулы Лагранжа это приведет не только к увеличению числа
слагаемых, но и к необходимости вычислять каждое из них заново. В то же время
для вычисления ![]() по формуле Ньютона (2.7.1)
достаточно добавить к
по формуле Ньютона (2.7.1)
достаточно добавить к ![]() лишь очередное слагаемое, так
как
лишь очередное слагаемое, так
как ![]() Если величина
Если величина ![]() мала, а
функция
мала, а
функция ![]() достаточно гладкая, то справедлива оценка:
достаточно гладкая, то справедлива оценка:
![]() из которой, с учетом предыдущего
равенства, следует, что
из которой, с учетом предыдущего
равенства, следует, что![]() Тогда величину
Тогда величину
![]() (2.7.3)
(2.7.3)
можно использовать для практической оценки погрешности интерполяции.
Согласно этой схеме интерполяционные многочлены любого вида вычисляются последовательно по формулам
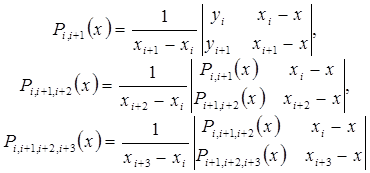 (2.8.1)
(2.8.1)
и так далее. Интерполяционный
многочлен ![]() -й степени, принимающий в точках
-й степени, принимающий в точках ![]() значения
значения ![]() запишется
следующим образом:
запишется
следующим образом:
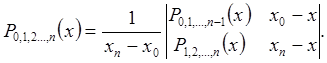 (2.8.2)
(2.8.2)
Действительно, из первой формулы (2.8.1) при ![]() сразу получаем
сразу получаем
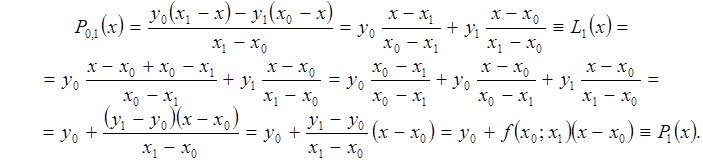
Остальные формулы проверяются
аналогично. Кроме того, мы получили, что ![]() . Это
действительно так по теореме о единственности интерполяционного многочлена
. Это
действительно так по теореме о единственности интерполяционного многочлена ![]() -й степени. Таким образом,
-й степени. Таким образом, ![]() тождественно совпадают и являются по сути
лишь разной формой записи единого интерполяционного многочлена
тождественно совпадают и являются по сути
лишь разной формой записи единого интерполяционного многочлена ![]() -й степени.
-й степени.
Схема Эйткена применяется там,
где не нужно общее выражение ![]() , а нужно лишь его
значение при конкретных
, а нужно лишь его
значение при конкретных ![]() , и при этом значения
функции даны в достаточно большом числе узлов. Вычисления по схеме Эйткена
удобно вести с помощью таблицы, аналогичной таблице конечных или разделенных
разностей:
, и при этом значения
функции даны в достаточно большом числе узлов. Вычисления по схеме Эйткена
удобно вести с помощью таблицы, аналогичной таблице конечных или разделенных
разностей:
|
|
|
|||
|
|
||||
|
|
|
|
||
|
|
|
|||
|
|
|
|
||
|
|
||||
|
|
|
|||
|
... |
... |
|
||
|
|
|
|
||
|
|
||||
|
|
|
Вычисления прекращают, если ![]() или если последовательные значения
или если последовательные значения ![]() совпадут в пределах заданной точности.
совпадут в пределах заданной точности.
Пример. Вычислить ![]() по схеме Эйткена в точке
по схеме Эйткена в точке ![]() , если
, если ![]() задана
таблицей:
задана
таблицей:
|
|
1.0 |
1.1 |
1.3 |
1.5 |
1.6 |
|
|
1.000 |
1.032 |
1.091 |
1.145 |
1.170 |
Составим таблицу и заполним по формулам (2.8.1) ее столбцы, начиная с четвертого:
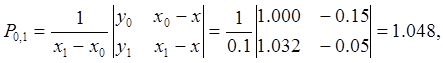
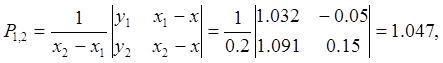
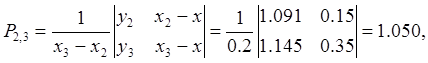
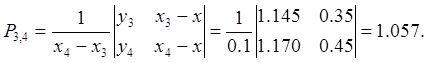
Следующий столбец таблицы заполняется аналогично:
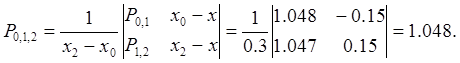
На этом вычисления можно
прекратить, так как ![]() совпадают до третьего знака,
следовательно,
совпадают до третьего знака,
следовательно, ![]() с точностью
с точностью ![]() Итоговая таблица с результатами вычислений
приведена ниже.
Итоговая таблица с результатами вычислений
приведена ниже.
|
|
|
|
|
|
|
|
0 |
1.0 |
1.000 |
-0.15 |
||
|
1.048 |
|||||
|
1 |
1.1 |
1.032 |
-0.05 |
1.048 |
|
|
1.047 |
|||||
|
2 |
1.3 |
1.091 |
0.15 |
||
|
1.050 |
|||||
|
3 |
1.5 |
1.145 |
0.35 |
||
|
1.057 |
|||||
|
4 |
1.6 |
1.170 |
0.45 |
Если интерполируемая функция задана на таблице с постоянным
шагом ![]() , то можно использовать связь между
конечными и разделенными разностями:
, то можно использовать связь между
конечными и разделенными разностями: 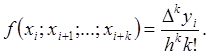 В
этом случае многочлен Ньютона можно записать несколько в ином виде:
В
этом случае многочлен Ньютона можно записать несколько в ином виде:
Пусть 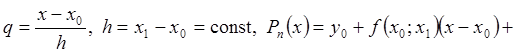
![]()
Преобразуем разделенные разности в конечные:
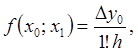 тогда
тогда
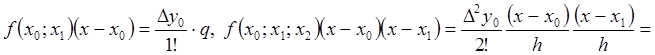
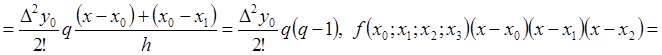
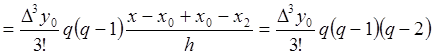 и так далее.
и так далее.
Тогда многочлен Ньютона можно переписать в следующем виде:
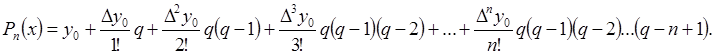 (2.10.1)
(2.10.1)
Эту формулу называют интерполяционным многочленом Ньютона с конечными разностями для интерполяции вперед. В ней используются только конечные разности, расположенные в верхней косой строке таблицы конечных разностей. Если использовать разности нижней косой строки, то аналогично получим многочлен Ньютона с конечными разностями для интерполяции назад:
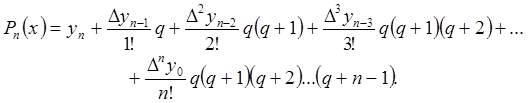 (2.10.2)
(2.10.2)
Пример. Вычислить 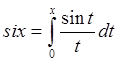 в
точках
в
точках ![]() , используя формулы (2.10.1) и (2.10.2)
при
, используя формулы (2.10.1) и (2.10.2)
при ![]() , если
, если
|
|
|
|
|
|
|
|
|
0.0 |
0.00000 |
|||||
|
19956 |
||||||
|
0.2 |
0.19956 |
-266 |
||||
|
19690 |
-257 |
|||||
|
0.4 |
0.39646 |
-523 |
10 |
|||
|
19167 |
-247 |
8 |
||||
|
0.6 |
0.58813 |
-770 |
18 |
|||
|
18397 |
-229 |
|||||
|
0.8 |
0.77210 |
-999 |
||||
|
17398 |
||||||
|
1.0 |
0.94608 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.