Вычислительная схема Эйткена. Интерполяционный многочлен Ньютона с конечными разностями. Интерполирование и экстраполирование данных, страница 2

Здесь 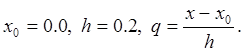  Для   используем формулу (2.10.1), так как значение   расположено в начале таблицы, тогда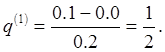   

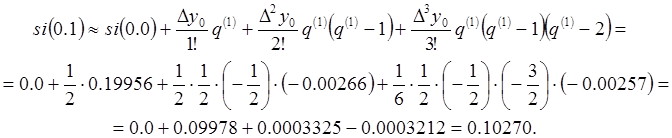
Для  лучше использовать формулу (2.10.2), так как  расположено ближе к нижнему краю таблицы. Тогда

2.11. Лабораторная работа № 3. Интерполирование и экстраполирование данных. Интерполяционный многочлен Ньютона

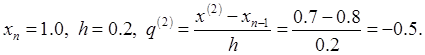
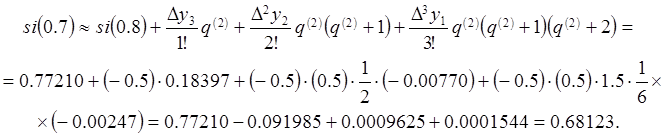
Интерполяционный многочлен Ньютона является другой формой записи единого интерполяционного многочлена. Применение многочлена Ньютона имеет практические преимущества по сравнению с формулой Лагранжа и в случае неравноотстоящих, и особенно в случае равноотстоящих узлов.

Интерполяционные многочлены Ньютона нужных степеней строятся по формулам (2.7.1) или (2.10.1) и (2.10.2).

Пример. Найти приближенное значение функции  при данном значении аргумента  с помощью интерполяционного многочлена Ньютона, если функция задана в неравноотстоящих узлах таблицы и :

Для вычисления интерполяционного многочлена по формуле (2.7.1) необходима таблица разделенных разностей, по которой можно вычислять разности до пятого порядка включительно по формулам

,  ,

.

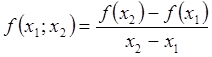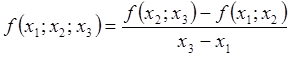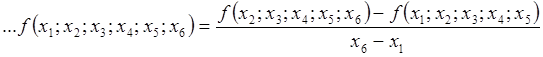Запишем получаемые конечные разности в виде таблицы, однако, в целях экономии места, не будем писать разности между строк  и . Тогда получим

Далее по формуле (2.7.1) вычисляем

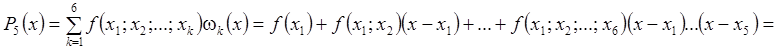
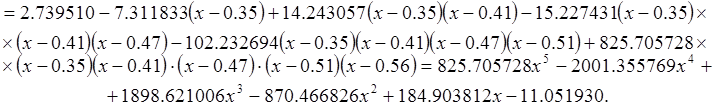
Подставляя теперь значение  вместо аргумента  в найденную формулу, вычислим приближенное значение функции

Задание № 1. Построить интерполяционный многочлен Ньютона по неравноотстоящей сетке узлов и найти приближенное значение интерполируемой функции  при значении аргумента .

I.

II.

III.