Математика \ Вычислительная математика

Вычислительная схема Эйткена. Интерполяционный многочлен Ньютона с конечными разностями. Интерполирование и экстраполирование данных, страница 4

Аналогично, для 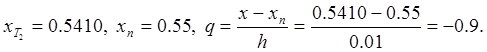 Воспользуемся формулой (2.10.2) для интерполяции назад:

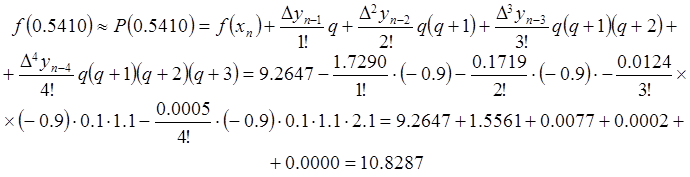
с той же точностью, что и в предыдущей формуле.

Задание № 2.Вычислить приближенное значение функции  по интерполяционной формуле Ньютона  для интерполяции вперед или назад.

I.

№ варианта

1

4.413

4.35

16.3597

6

6.085

4.60

17.7334

11

5.218

4.85

18.7686

16

6.480

5.10

20.0334

21

4.390

5.35

22.2846

26

6.020

5.60

23.5973

5.85

25.0811

6.10

26.5278

6.35

28.3944

6.60

29.9902

II.

№ варианта

2

1.210

1.15

66.1659

7

4.680

1.55

63.9989

12

2.000

1.95

61.9658

17

3.870

2.35

60.0551

22

2.411

2.75

58.2558

27

3.275

3.15

56.5583

3.55

54.6807

3.95

52.7220

4.35

50.5229

4.75

48.1091

III.

№ варианта

3

0.105

0.10

1.2618

8

0.121

0.16

1.2764

13

0.625

0.22

1.2912

18

0.438

0.28

1.3062

23

0.534

0.34

1.3213

28

0.229

0.40

1.3366

0.46

1.3521

0.52

1.3677

0.58

1.3836

0.64

1.3995

IV.

№ варианта

4

1.871

1.350

4.2556

9

1.369

1.355

4.3533

14

1.382

1.360

4.4552

19

1.394

1.365

4.5618

24

1.354

1.370

4.6734

29

1.362

1.375

4.7904

1.380

4.9131

1.385

5.0419

1.390

5.1778

1.395

5.3202

V.

№ варианта

5

1.285

1.20

10.6044

10

1.211

1.21

11.3276

15

1.272

1.22

11.9671

20

1.228

1.23

12.5324

25

1.263

1.24

13.0328

30

1.237

1.25

13.4776

1.26

13.8759

1.27

14.2367

1.28

14.5688

1.29

14.8809

* Александр Крег Эйткен (1895-1967) - английский математик.

Скачать файл