Вычислительная схема Эйткена. Интерполяционный многочлен Ньютона с конечными разностями. Интерполирование и экстраполирование данных, страница 3

IV.

№ варианта
4	3.905	3.50	33.1154
9	4.110	4.55	34.8133
14	5.995	5.60	36.5982
19	7.213	6.20	38.4747
24	9.115	7.75	40.4473
29	10.050	8.80	42.5211
		9.45	44.7012
		10.95	46.9931

№ варианта
5	1.090	1.01	12.6183
10	1.250	1.08	12.7644
15	1.275	1.11	12.9122
20	1.316	1.21	13.0617
25	1.488	1.26	13.2130
30	1.343	1.33	13.3660
		1.46	13.5207
		1.51	13.8357

Конечные разности практически вычисляются значительно проще разделенных, поэтому исходная таблица может содержать заметно больше узлов при тех же вычислительных затратах.

Пример. Используя интерполяционную формулу Ньютона с конечными разностями для интерполяции вперед и назад, вычислить значения функции при данных значениях аргумента

0.45	0.46	0.47	0.48	0.49	0.50
20.1946	19.6133	18.9425	18.1746	17.3010	16.3123
0.51	0.52	0.53	0.54	0.55	0.56
15.1984	13.9484	12.5508	10.9937	9.2647	7.3510

Составим таблицу конечных разностей. Ограничимся при этом разностями четвертого порядка, так как они практически постоянны. Для вычисления значения функции при воспользуемся формулой Ньютона для интерполяции вперед (2.10.1). При этом разности из таблицы лучше всего брать стоящие по той диагонали, которая ближе всего расположена к . В таблице разностей эта диагональ подчеркнута. Тогда 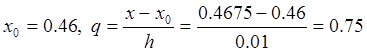и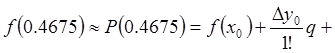

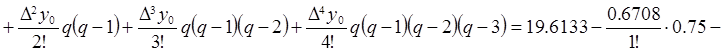
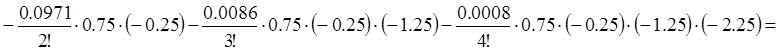
с точностью


0.45	20.1946
		-0.5813
0.46	19.6133		-0.0895
		-0.6708		-0.0076
0.47	18.9425		-0.0971		-0.0010
		-0.7679		-0.0086
0.48	18.1746		-0.1057		-0.0008
		-0.8736		-0.0094
0.49	17.3010		-0.1151		-0.0007
		-0.9887		-0.0101
0.50	16.3123		-0.1252		-0.0008
		-1.1139		-0.0109
0.51	15.1984		-0.1361		-0.0006
		-1.2500		-0.0115
0.52	13.9484		-0.1476		-0.0004
		-1.3976		-0.0119
0.53	12.5508		-0.1595		-0.0005
		-1.5571		-0.0124
0.54	10.9937		-0.1719		-0.0004
		-1.7290		-0.0128
0.55	9.2647		-0.1847
		-1.9137
0.56	7.3510

1 2 3 4

Скачать файл