Даются методические указания к лабораторным работам по исследованию точности и стабильности изготовления ЭА.
Лабораторная работа № 1
ИССЛЕДОВАНИЕ ТОЧНОСТИ ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ
ПРОИЗВОДСТВА ЭА
Цель работы: изучение методики анализа и расчета основных показателей точности технологических процессов производства ЭА.
Содержание работы: уяснить поставленную задачу. Ознакомиться с установкой для моделирования потока измерений. Рассчитать числовые характеристики точности и проанализировать распределение вероятностей погрешностей контролируемого параметра.
Методические указания по подготовке к работе
Под точностью технологического процесса ТП понимается свойство ТП,
обусловливающее близость действительных и номинальных заданных значений
параметров производимой продукции [l]. Мерой точности является величина
погрешности, определяемая как отклонение![]() действительного
значения параметра X от номинального значения Хном этого параметра,
выраженная в единицах измеряемой величины [2],
действительного
значения параметра X от номинального значения Хном этого параметра,
выраженная в единицах измеряемой величины [2], ![]() (рис.
1, а ). Действительное значение параметра - величина случайная, поэтому
погрешность также величина случайная, задаваемая плотностью распределения W(
(рис.
1, а ). Действительное значение параметра - величина случайная, поэтому
погрешность также величина случайная, задаваемая плотностью распределения W(![]() ) или числовыми характеристиками,
чаще всего математическим ожиданием
) или числовыми характеристиками,
чаще всего математическим ожиданием ![]() и среднеквадратическим
отклонением
и среднеквадратическим
отклонением ![]() которые характеризуют соответственно
систематическую и случайную составляющие погрешности.
которые характеризуют соответственно
систематическую и случайную составляющие погрешности.
Причинами систематической погрешности являются: неточная на наладка технологического оборудования (ТО), разлаживаиие ТО вследствии износа и старения элементов ТО, ослабление механических креплений, монотонного изменения технологических режимов параметров окружающей среды ит.д. [3].
Причинами случайной погрешности являются: неточность работы ТО , случайные изменения технологических режимов параметров окружающей среды, разброс параметров комплектующих изделий и материалов и т. д. [3] .
Величина предельно допустимого отклонения - допуск ![]() или
или ![]() ,
где
,
где ![]() и
и ![]() -
верхнее и нижнее предельно допустимые значения параметра, обычно задаются.
-
верхнее и нижнее предельно допустимые значения параметра, обычно задаются.
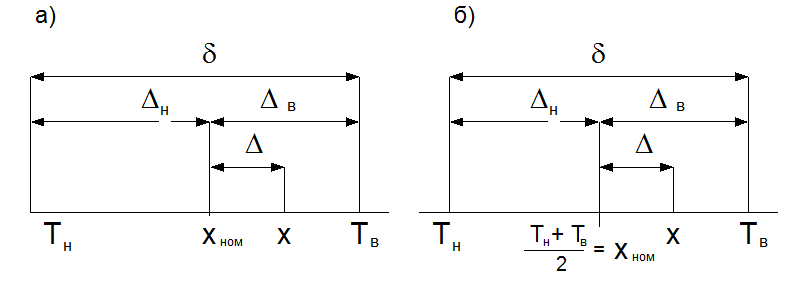 Рис. 1. К понятию погрешности и
допуска: а – номинальное значение совпадает с серединой поля допуска; б –
номинальное значение не совпадает с серединой поля допуска.
Рис. 1. К понятию погрешности и
допуска: а – номинальное значение совпадает с серединой поля допуска; б –
номинальное значение не совпадает с серединой поля допуска.
Полем допуска называется величина ![]() ,
(рис.1,а). При несимметричном расположении поля допуска относительно
номинального значения при расчете погрешности вместо номинального значения
параметра принимают середину поля допуска
,
(рис.1,а). При несимметричном расположении поля допуска относительно
номинального значения при расчете погрешности вместо номинального значения
параметра принимают середину поля допуска ![]() (рис.
1, б).
(рис.
1, б).
Для налаженного, нормально протекающего ТП, должно выполняться с заданной
достаточно близкой к 1 вероятностью соотношение ![]() .
.
В процессе анализа точности ТП необходимо установить [2]:
- величины случайных и систематических
погрешностей, характеризуемые соответственно ![]() и
и
![]() ;
;
- функции распределения погрешностей;
- зависимости между погрешностями для различных параметров.
На практике величины ![]() и
и ![]() приходится определять приближенно,
заменяя их соответственно выборочными средним значением
приходится определять приближенно,
заменяя их соответственно выборочными средним значением ![]() и
среднеквадратическим или стандартным отклонением S , найденными по
ограниченному числу измерений n .
и
среднеквадратическим или стандартным отклонением S , найденными по
ограниченному числу измерений n .
Величины ![]() и S определятся по
формулам:
и S определятся по
формулам:
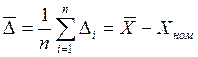 , где
, где 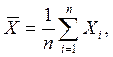 (1)
(1)
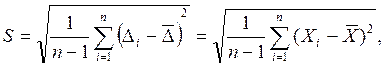 (2)
(2)
где ![]() и
и ![]() - действительные значения параметра
и погрешности для i-го изделия.
- действительные значения параметра
и погрешности для i-го изделия.
На практике применяются также нормированные характеристики точности: коэффициент точности КТ и коэффициент вариации КВ
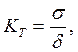
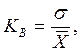 (3)
(3)
На практике часто случайная погрешность контролируемого паpaметра ЭА и ее элементов распределена по нормальному закону (рис. 2)
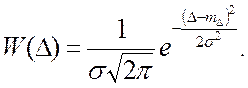 (4)
(4)
Правомочность использования нормального распределения обусловлена тем, что при современных многооперационных ТП производства ЭА выполняются условия действия центральной предельной теоремы вероятностей – большое число независимых не изменяющихся во времени первичных погрешностей, из которых образуется результируюшая.
 Рис.2. Нормальное
распределение погрешности: а – ТП разлажен; б – ТП налажен.
Рис.2. Нормальное
распределение погрешности: а – ТП разлажен; б – ТП налажен.
Для нормальной случайной величины принято задавать поле рассеяния в
пределах + 3![]() от величины
от величины ![]() . В пределах поля рассеяния
случайная величина находится с вероятностью 0,997 (рис.3).
. В пределах поля рассеяния
случайная величина находится с вероятностью 0,997 (рис.3).
Для анализа распределения погрешностей строится гистограмма распределения
[3]. Из серии n измеренных значений выбираются максимальное ![]() и минимальное
и минимальное ![]() .
.
Весь диапазон значений ![]() ….
….![]() разбивается на интервалы, количество
которых определяется по приблизительной формуле к = 3,3 + lgn.
Рассчитывается частота попадания измерений в каждый интервал:
разбивается на интервалы, количество
которых определяется по приблизительной формуле к = 3,3 + lgn.
Рассчитывается частота попадания измерений в каждый интервал:
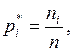
![]() - число попаданий измеренных
значений в i-й интервал. На основаниях полученных интервалов строятся
прямоугольники высотой
- число попаданий измеренных
значений в i-й интервал. На основаниях полученных интервалов строятся
прямоугольники высотой ![]() .
.
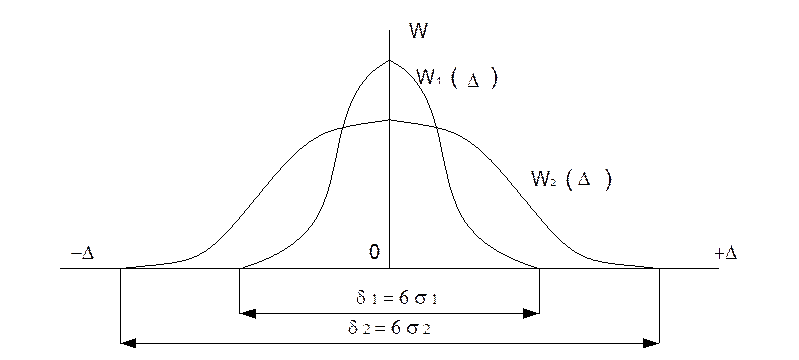
Рис. 3. К понятию поля рассеяния погрешности.
Совокупность прямоугольников для всех интервалов образует гистограмму
(рис. 4). По данным построения гистограммы можно также определить ![]() и S по формулам:
и S по формулам:
![]()
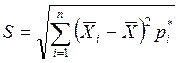 , (5)
, (5)
где 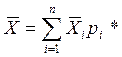 ;
; ![]() -
середина i-го интервала.
-
середина i-го интервала.
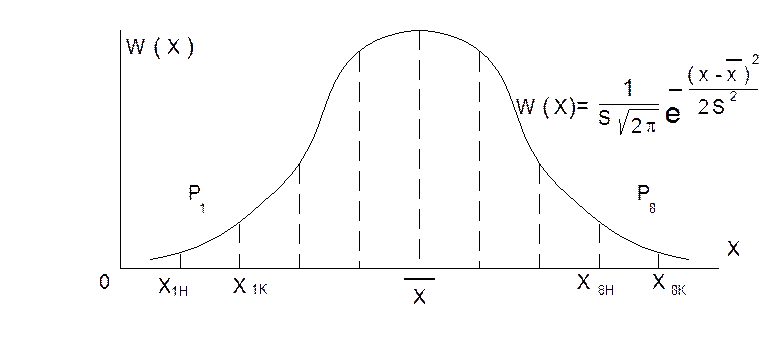
Рис. 4. К опредерению P i.
После построения гистограммы необходимо проанализировать степень соответствия реального распределения погрешностей какому-то теоретическому. В качестве последнего чаще всего выбирают нормальное распределение. Отклонение от распределения погрешностей, характерное для данного ТП может служить сигналом разладки ТП.
Для определения степени соответствия реального распределения нормальному
можно воспользоваться критерием ![]() [3, 5], для чего
необходимо рассчитать величину
[3, 5], для чего
необходимо рассчитать величину
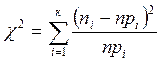 ,
(6)
,
(6)
![]() - вероятность попадания случайной величины в i –й интервал в соответствии с нормальным законом распределения
(рис. 5):
- вероятность попадания случайной величины в i –й интервал в соответствии с нормальным законом распределения
(рис. 5):
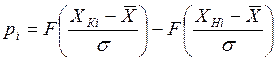 ,
(7)
,
(7)
где ![]() и
и ![]() -
конец и начало i -го интервала соответственно;
-
конец и начало i -го интервала соответственно;
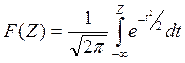 - табулированная функция [3].
- табулированная функция [3].
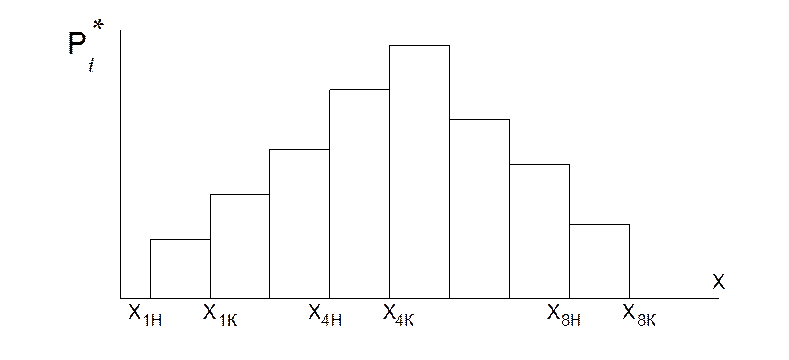
Рис. 5. Гистограмма распределения (к = 10).
После расчета величины ![]() по формуле (6) необходимо
обратиться к таблицам
по формуле (6) необходимо
обратиться к таблицам ![]() -распределения [ 3],
принимая во внимание, что в данном случае число степеней свободы m = к
- 3. Задавая определенную степень доверия выводу о согласии опытного
распределения нормальному (
-распределения [ 3],
принимая во внимание, что в данном случае число степеней свободы m = к
- 3. Задавая определенную степень доверия выводу о согласии опытного
распределения нормальному (![]() ), из таблиц
), из таблиц ![]() -распределения можно получить граничное
-распределения можно получить граничное
![]() , при этом, если
, при этом, если ![]() <
< ![]() ,
то гипотеза о нормальном распределении может быть принята.
,
то гипотеза о нормальном распределении может быть принята.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.