Исследование точности технологических процессов производства электронных аппаратов, страница 3

- износ и старение элементов технологического оборудования;

- изменение параметров окружающей среды (температуры, влажности, давления,  изменения состава атмосферы и т. д.);

- загрязнения рабочих камер технологического оборудования;

- изменения  параметров сырья и комплектующих изделий;

- субъективные факторы, связанные с ручными операциями (утомляемость,  ослабление внимания и т. д.).

Следствием нестабильности ТП является расширение поля рассеяния значений параметра,  постольку в общем случае увеличивается как постоянная составляющая погрешности , так и случайная ,  (рис. 1а, 2а.). Это требует расширения допуска на контролируемый параметр, приводящего к снижению качества ЭА. При неизменном допуске на контролируемый параметр, при нестабильности увеличивается число бракованных изделий, параметры которых оказываются вне поля допуска , т.е. увеличиваются технологические потери на брак (рис. 1,б, 2,б).

 Для уменьшения вредного влияния нестабильности ТП производят регулирование ТП, либо по истечении определенного времени, либо после выпуска определенного числа изделий, либо по данным периодического контроля ТП. Последний случай носит название статистического регулирования ТП.

Анализ стабильности ТП можно производить как по одной реализации, так в по совокупности нескольких реализаций [6].

Одна реализация процесса изменения контролируемого параметра соответствует одной партии последовательно изготавливаемых изделий на одном ТО при одной его настройке.

Систематическая погрешность для одной реализации в любой момент времени  , определяется как среднее значение погрешности контролируемого параметра, определяемое по мгновенной выборке в момент     .

Мгновенной выборкой называется выборка, составленная из изделий, произведенных последними к моменту отбора в течение достаточно короткого интервала времени [1]. Число изделий в выборке  20.

За величину случайной погрешности в -й момент времени принимается величина мгновенного поля рассеяния, охватывающая 99,73%  всех значений контролируемого параметра при нормальном их распределении и равное  где - среднее квадратическое отклонение, определяемое по мгновенной выборке в момент времени .

Систематическая  и случайная погрешности при анализе стабильности должны быть определены в виде функций   или и  или  .

Как правило, эти функции монотонные и медленно меняющиеся по сравнению с периодом выборок.  Они могут быть хорошо описаны простыми функциями t , например, полиномами 1-й и 2-й степеней, которые подбираются по методу наименьших квадратов [6] (МНК).

В соответствии о МНК аппроксимирующая функция  подбирается таким образом, чтобы обеспечивалось

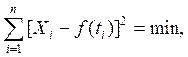
где X _i   - экспериментально полученные значения в моменты  .

В тех случаях, когда по условиям производства имеется возможность получить более 10 реализаций случайного процесса, каждая из которых соответствует либо своей настройке ТО, либо разным однотипным образцам ТО,  систематическая и случайная погрешности в момент времени  рассчитываются усреднением по ансамблю реализаций  в момент времени  t . При этом для любого момента   справедливо :

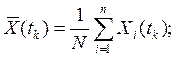                                           (1)

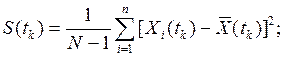                      (2)

где    - число реализаций (партий);

 - значение контролируемого параметра для -й реализации (партии) в момент   .

Систематическая погрешность будет равна    , где  - номинальное заданное значение параметра.

Функции  и , выравнивающие значения  и  на интервале k = 1,2,…n , также определяются по MНIK.

На практике для оценки стабильности часто пользуются нормированными характеристиками случайных и систематических погрешностей за межнастроечный период по мгновенным выборкам.

Показатель смещения среднего значения контролируемого параметра рассчитывается по формуле

 ,                                    (3)

где  и   - соответственно среднее значение последней перед новой настройкой и первой мгновенной выборки.

Изменение среднеквадратического отклонения характеризуется показателем межнастроечной стабильности:

  ,                                       (4)

где  и  - средние квадратические отклонения соответственно в первой и последней мгновенных выборках.

Зная функции    и , можно решать задачу прогнозирования поля рассеяния измерений в  любой момент времени :

  ,

и сопоставлять его с положением поля допуска  .  Если по данным прогнозирования поле рассеяния оказывается за пределами поля допуска, то производят заблаговременно предупредительную настройку технологического оборудования.

Если   и  получены по МНК с использованием сглаживающих полиномов первого и второго порядков и период измерений постоянен, то для получения оценок прогноза на интервал равный одному периоду имерений, можно воспользоваться формулой

,

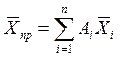где  - среднее значение в момент i -го измерения; n -   число сглаживаемых измерений;   Ai - постоянные коэффициенты, зависящие от n  и вида полинома (табл.1).

Для прогноза среднеквадратического отклонения также применима формула (5) и табл.1.

2.         Описание  лабораторной установки

Аналогично работе № 1.

3.         Порядок выполнения работы

3.1. Проверка работы лабораторной установки

Аналогично подразл.3.1 работы № 1.

3.2. Анализ стабильности по одной реализация

а) Поставить переключатель СРЕДНЕЕ в левое крайнее положение, переключатель ДИСПЕРСИЯ - в положение 3. Записать 20 Последовательных  чисел. Поставить переключатель СРЕДНЕЕ в соседнее положение. Записать 20 последовательных чисел. Пройти все оставшиеся положения переключателя    , записывая каждый раз 20 чисел. Результаты занести в табл.2.

Таблица 2

№ положения	№ числа
	1	2	…	20
1 2 . . . 7

б) Аналогично получить и записать 5 групп по 20 чисел, меняя положения переключателя ДИСПЕРСИЯ.

Результаты занести в табл.3.

Таблица 3

Положения переключателя - р	№ числа в реализации	№ реализации
		1	2	3	4	5
1	1 2 3 4
2 . . . 5	5 . . . 20