Исследование точности технологических процессов производства электронных аппаратов, страница 4

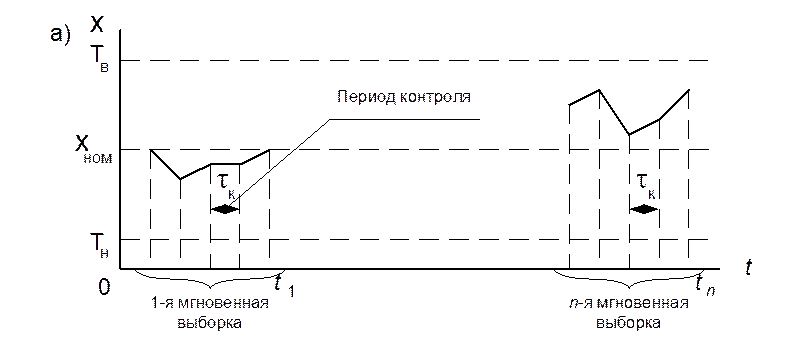
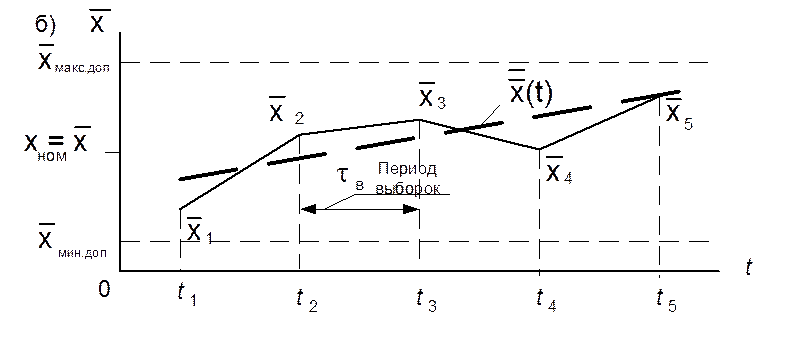
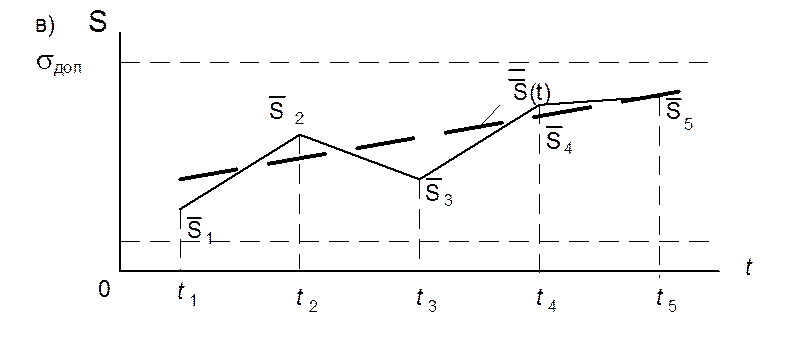
Рис.3. Анализ нестабильности по одной реализации: а – реализация последовательности измерений; б, в –изменения среднего значения и среднеквадратического отклонения

3.3. Анализ стабильности по ансамблю реализаций

а) Поставить переключатель СРЕДНЕЕ в левое крайнее положение, переключатель ДИСПЕРШЯ - в положение 3, тумблер АВТОМАТИЧЕСКАЯ - РУЧНАЯ - в положение РУЧНАЯ. Для 5 последовательных положений переключателя СРЕДНЕЕ получить по 4 числа,  пользуясь кнопкой ручного запуска имитатора случайных чисел.  Повторить указанные операции 5 раз и получить 5 реализаций объемом в 28 чисел каждая. Результаты записать в табл. 3.

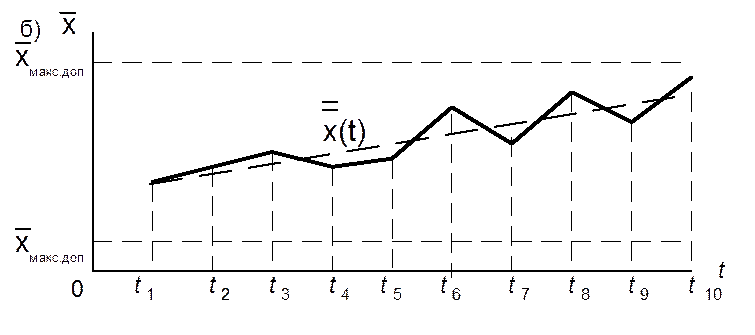
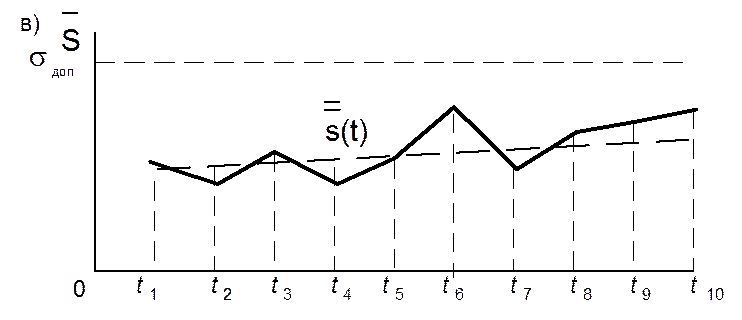
Рис.4. Анализ нестабильности по нескольким реализациям: а – совокупность реализаций; б, в – изменения среднего значения и среднеквадратического отклонения

4. Обработка результатов измерений

4.1. Определение характеристик стабильности по одной реализации;

а) По данным табл.2 определить среднее значение для каждой мгновенной выборки из 20 чисел, соответствующей определенному положению переключателя  по формуле 3, работа № 1.

б)         По полученным 7 значениям средних значений    постронть по  МНК  (Приложение 2) функцию   для сглаживающего полинома первой степени      , где     определяются по формулам в Приложении 2 [5].

в)         Аналогично, пользуясь табл.3, для каждой мгновенной выборки из 20 чисел определить среднеквадратическое отклонение по формуле (4) работы № 1 и построить сглаживающий полином первой степени ;

г)         Найти значение оценки прогноза   по формуле (5)  с помощью табл.1 для 5 значений мгновенных средних и среднеквадратических значений.

4.2. Определение характеристик стабильности по нескольким реализациям

а)         По данным табл.4 найти средние значения по всем реализациям для каждого номера числа .

б)         Усреднить полученные значения для каждого положения переключателя      получить значения  .

в)         По полученным 5-ти значениям    построить по МНК (Приложение 2) функцию  для сглаживающего полинома первой степени             (см подр.4.1.б);

г)         Найти значение оценки прогноза в соответствии о подр.4.1 .

5. Задание по УИРС

а) По подр. 4.1,б функцию  получить по МНК для сглаживающего полинома 2-й степени, определить дисперсии погрешностей сглаживания пo полиномам первой и второй степени  сравнивая дисперсии, сделать вывод о наилучшем полиноме сглаживания.

б) При анализе стабильности по одной реализации проанализировать точность прогнозирования     по МНК при изменении числа обрабатываемых наблюдений с 5 по 7. пользуясь формулой (5)и табл.1.

в) Провести  аналогичный сравнительный анализ при числе наблюдений  для сглаживающего полинома первой и второй степени.

6. Требования к отчету

Отчет должен содержать: формулировку цели работы, расчетные формулы, таблицы измерений и расчетных характеристик, зависимости ,  для случаев одной реализации и  нескольких реализаций,  значения оценок прогноза, выводы по работе, содержащие числовые характеристики стабильности  и .

Библиографический список

1. ГОСТ 15895-77. Статистические методы управления качеством продукции. Термины и определения. M.: Издательство стандартов , 1977.

2. ГОСТ 16304-74. Управление технологическими процессами. Контроль точности технологических процессов. М.: Издательство стандартов, 1974.

3. Глудкин О.П., Черняев В.Н.. Анализ и контроль технологических процессов производства РЭА. М.: Радио и связь, 1983.

4. ГОСТ 16467-70. Статистические показатели точности и стабильности технологических операций. Методы расчета. М.: Издательство стандартов, 1970.

5. ГОСТ 11006-74. Правила проверки согласия опытного распределения с теоретическим. М.: Издательство стандартов, 1974.

6. ГОСТ 16305-74. Контроль точности технологических процессов. Методы оценки точности в условиях серийного и массового производства. М.: Издательство стандартов, 1974.

7. Контроль и регулировка РЭА. Лабораторные работы   /Дмитриевский Е.С., Илларионов О.И., Лебедев K.М. /ЛИАП.Л., I980.

Приложение I

ПРОГРАММЫ ДЛЯ ОБРАБОТКИ РЕЗУЛЬТАТОВ НАБЛЮДЕНИЙ НА МИКРОКАЛЬКУЛЯТОРЕ (MK-61, MK-52)

I.  Вычисление среднего  значения и среднеквадратического отклонения.

Расчеты производятся по формулам:

- среднее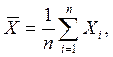

- среднеквадратическое отклонение .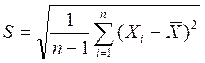

Приложение 2

ОБРАБОТКА РЕЗУЛЬТАТОВ НАБЛЮДЕНИЙ ПО МЕТОДУ НАИМЕНЬШИХ КВАДРАТОВ( МНК)

Если имеется последовательность значений исследуемой величины  ,     полученных в моменты временя   , то сглаживающие полиномы необходимо получать по методу наименьших квадратов (МНК),.

При использовании сглаживающего полинома первой степени  ,        коэффициенты определяются по формулам [6]:

   ;

  .

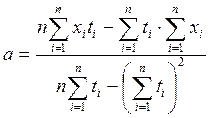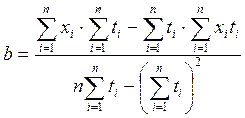В лабораторной работе сглаженные кривые используются для иллюстрации относительных изменений во времени среднего и среднеквадратического отклонений в ходе наблюдений, поэтому начало отсчета времени можно выбрать произвольно, в частности, так, чтобы 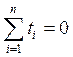. При одинаковых интервалах времени между наблюдениями  моменты измерений (для n = 5) будут  расположены в соответствии о таблицей:

Величина
Величина			0

Указанный подход справедлив при нечетных n .

Формулы для  a   и  b    упрощаются:

  ;      .

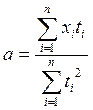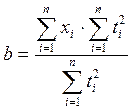При использовании сглаживающего полинома 2-й степени  и условия 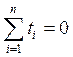 коэффициенты определяются по формулам:

  ;           ;                .

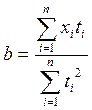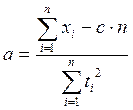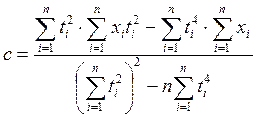Выбор вида сглаживающей функции необходимо производить, исходя из величины дисперсии      разброса наблюдений относительно сглаживающей функции . Для сглаживающих полиномов  k-й степени:   

   .

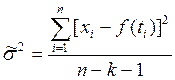Оглавление

Работа № 1. Исследование  точности технологических процессов производства ЭА

Работа № 2. Исследование стабильности технологических процессов производства ЭА

Библиографический список           

Приложения