cos x, ln 5x, x2-3x+5 для каждой из которых задан интервал [a, b] и шаг h.
Program pr_type;
type func=function(x: real): real; {объявлен процедурный тип для функции с одним вещественным аргументом и результатом вещественного типа}
{$F+} {директива дальнего вызова включена}
function f1(x: real): real;
begin
f1:=cos(x)
end;
function f2(x: real): real;
begin
f2:=ln(5*x)
end;
function f3(x: real): real;
begin
f3:=sqr(x)-3*x+5
end;
{$F-} {директива дальнего вызова отключена }
{***********процедура вывода таблицы произвольной функции на заданном отрезке с заданным шагом*********************}
procedure print_table(f: func; a, b, h: real);
var xp: real;
begin
xp:=a;
while xp<=b do
begin
writeln(xp:8:2, f(xp):8:2);
xp:=xp+h
end;
writeln
end;
{****** основная программа ******}
begin
print_table(f1, -3.14, 3.14, 0.5);
print_table(f2, 0.5, 125, 0.2);
print_table(f3, -5, 5, 0.5);
end.
Если требуется вывести не все таблицы, а таблицу какой-то одной функции, можно воспользоваться процедурной переменной. В этом случае основная программа будет выглядеть следующим образом.
var fn: func; i: integer;
begin
write(‘введите номер функции ’); readln(i);
case i of
1: fn:=f1;
2: fn:=f2;
3: fn:=f3
end;
print_table(f, 1, 5, 0.5)
end.
 |
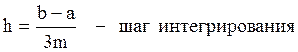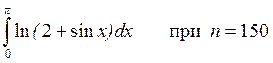
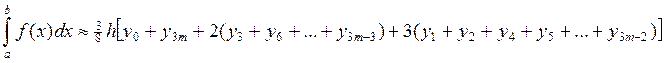Написать подпрограмму вычисления значения определенного
интеграла любой функции y=f(x) на отрезке [a, b] по формуле Ньютона:
где n=3m - число разбиений отрезка кратное 3.
x0=a, x3m=b, xi=x0+ih (i=0, 1, …, 3m)
yi=f(xi) (i=0, 1, …, 3m) - значение функции в точке xi
Используйте эту подпрограммe для вычисления интеграла
program vich_int_newt;
type func=function(xx:real):real;
{$f+}
function f1(x:real):real;
begin
f1:=ln(2+sin(x))
end;
function f2(x:real):real;
begin
f2:=x*x;
end;
{$f-}
function Integral_Newton(a,b:real; n:integer; f:func): real;
var h,xi,yi,s1,s2,s3:real; i,m:integer;
begin
m:=n div 3;
h:=(b-a)/(3*m);
s1:=f(a)+f(b); s2:=0; s3:=0;
xi:=a;
for i:=1 to (3*m-1) do
begin
xi:=xi+h;
yi:=f(xi);
if i mod 3=0 then s2:=s2+yi
else s3:=s3+yi;
end;
Integral_Newton:=3/8*h*(s1+2*s2+3*s3)
end;
begin
writeln('Вычисление интеграла методом Ньютона');
writeln('интеграл функции ln(2+sinx) на интервале ',0,' ',Pi);
writeln('равен ', Integral_Newton(0,Pi,150,f1):3:3);
readln
end.
9.Распределение памяти в системе Турбо-Паскаль. Динамическая память.
Постановка задачи.
Проблема: при решении задач, в которых предполагается обработка массивов, встает вопрос об объявлении типов массива, определении переменных и выделении памяти для хранения элементов массивов. Например, объявлен тип:
const number = 15000;
type massiv = array[0..number] of longint;
var chisla : massiv;
Какие бы конкретные обработки не включались в данной задаче, пройдет все. Однако, проблемы начнутся в том случае, если потребуется обработка не 15000, а 20000 тысяч элементов типа longint. При попытке запуска данной редакции той же программы возникнет сообщение:
«Error 22: Structure too large.»
Это значит: «Ошибка 22: Структура чересчур объемиста»
Теперь в меню Help можно выбрать пункт Error messages, а затем выбрать пояснение о сути ошибки. Оно гласит, что максимальный размер для структурированных типов составляет 65520 байт. Что это значит? Для хранения одного элемента типа longint требуется 4 байта памяти, а для массива из 15000 элементов – 60000 байт. При этом раскладе программа работает правильно. Если же потребуется хранение 20000 элементов, то это значит и 80000 байт памяти. Таким образом, превышается максимальный объем памяти. Выход из данной ситуации, в том числе и для работы с массивами, большими 20000 элементов, в языке Паскаль возможен и представляется в виде использования динамической памяти и указателей.
Динамическая память.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.